Dihedral angle

Dihedral angle refers to the angle formed between two intersecting planes in three-dimensional space. In the context of chemistry and molecular biology, dihedral angles are crucial for understanding the three-dimensional structures of molecules and proteins, influencing their properties and interactions. In mathematics and engineering, dihedral angles play a significant role in the study of polyhedra and the design of various structures.

Definition

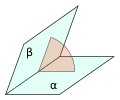
A dihedral angle is defined as the angle between two planes, which can be determined by selecting two intersecting lines, one from each plane, and measuring the angle between these lines. This angle provides a measure of the spatial orientation between the two planes. In a more practical sense, in molecular geometry, it is the angle between two planes formed by three atoms each, with two atoms shared between the planes.

Measurement

The measurement of dihedral angles can be performed using various methods, depending on the context. In molecular biology, computational tools and X-ray crystallography are commonly used to determine the angles between atoms in a molecule. In engineering and mathematics, geometric principles and tools like protractors or computational models are employed.

Importance in Molecular Biology

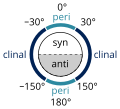
In molecular biology, dihedral angles, also known as torsion angles, are essential for understanding the conformation of biomolecules. These angles influence the folding and function of proteins, the double helix structure of DNA, and the efficacy of drug molecules. The Ramachandran plot, a tool used to visualize the conformational space of amino acids in proteins, is based on the phi (φ) and psi (ψ) dihedral angles.

Applications in Chemistry

In chemistry, dihedral angles are important for predicting the physical and chemical properties of molecules. The angle affects the molecule's polarity, reactivity, and overall shape, which in turn influences its interactions with other molecules. Understanding dihedral angles is crucial for the design of new pharmaceuticals and materials.

Engineering and Design

In the field of engineering, dihedral angles are important in the design of mechanical joints, bridges, and architectural structures. They determine the stability and stress distribution within the structure. In aerospace engineering, the dihedral angle of an airplane's wings significantly affects its aerodynamic properties and stability during flight.

Mathematical Significance

Dihedral angles are also of interest in pure mathematics, particularly in the study of polyhedra and tessellations. They are key to understanding the geometry and symmetry of three-dimensional shapes.

See Also

• Molecular geometry
• Protein structure
• X-ray crystallography
• Ramachandran plot

This article is a medical stub. You can help WikiMD by expanding it!
Most recent articles Ongoing trials	Wikipedia

   This article is a geometry-related stub. You can help WikiMD by expanding it!

This article is a stub related to chemistry. You can help WikiMD by expanding it!

   This article is a molecular biology stub. You can help WikiMD by expanding it!

• 

  Dihedral angle illustration

• 

  Spherical bond dihedral angle

• 

  Synantipericlinal conformation

• 

  Newman projection of butane

• 

  Sawhorse projection of butane

• 

  Dihedral angles of Butane

• 

  Protein backbone Phi, Psi, Omega angles