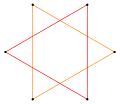
Stellation

Stellation is the process of extending the faces of a polyhedron in a symmetrical way until they meet to form a new polyhedron. It is a concept in geometry that generates a vast array of complex shapes and structures from simpler ones. The term "stellation" was first introduced in the early 20th century by the British mathematician and scientist Arthur Cayley. The process has since been explored in depth by various mathematicians, including H.S.M. Coxeter, who provided a comprehensive analysis of stellation in higher dimensions.

Overview

Stellation is closely related to the concepts of duality and polyhedron reciprocation, where the vertices of one polyhedron correspond to the faces of another and vice versa. Through stellation, one can construct new polyhedra that share the same symmetry properties as the original but exhibit more complex structures. The process involves extending the faces of the original polyhedron until they intersect with extensions from other faces, forming new edges and vertices.

Mathematical Definition

Mathematically, stellation can be described using the concept of the stellating vector, which determines the direction and magnitude by which the faces of the polyhedron are extended. The set of all possible stellations of a polyhedron forms a stellation diagram, which represents the combinatorial possibilities of face extension and intersection.

Types of Stellations

Stellations can be categorized based on the polyhedra being stellated. The most commonly studied are the stellations of the Platonic solids, which include the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. Each of these solids has a unique set of stellations, with the dodecahedron and icosahedron having the most complex and numerous stellations due to their higher number of faces and symmetry.

Applications

Stellation has applications in various fields, including architecture, art, and molecular modeling. In architecture, stellated forms are used to create complex, aesthetically pleasing structures that are also structurally sound. In art, stellation is employed to generate intricate sculptures and designs. In molecular modeling, stellation principles are used to understand and predict the shapes of complex molecules and crystals.

Examples

One of the most famous examples of stellation in architecture is the Eden Project in Cornwall, England, where the geodesic domes are based on stellated polyhedra. In art, the works of M.C. Escher often incorporate stellated forms, blending mathematical precision with artistic creativity.

See Also

• Polyhedron
• Geometric shape
• Convex and concave polyhedra

References

   This article is a mathematics-related stub. You can help WikiMD by expanding it!

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation

• 

  Stellation