Least squares

Linear least squares2

X33-ellips-1

Bendixen - Carl Friedrich Gauß, 1828

Linear Residual Plot Graph

Parabolic Residual Plot Graph

Heteroscedasticity Fanning Out

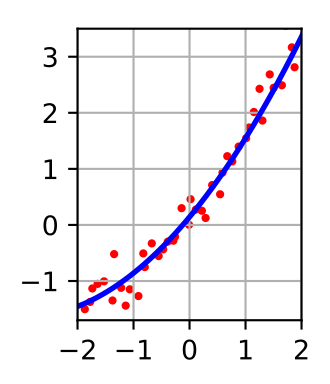
Least squares is a mathematical approach used in statistics, mathematics, and engineering to find the best-fit curve or line through a set of points in a manner that minimizes the sum of the squares of the differences between the observed values and the values provided by the model. This method is widely used in data fitting and is fundamental in the field of regression analysis, where it helps in estimating the unknown parameters in a linear model.

Overview

The least squares method can be applied in simple linear regression, multiple regression, and non-linear regression. It is particularly useful in situations where the data contains measurement errors or the number of data points is greater than the number of parameters to be estimated. The least squares criterion is based on the principle of minimizing the sum of the squares of the residuals, which are the differences between the observed values and the values predicted by the model.

Mathematical Formulation

The mathematical formulation of the least squares method for a linear model \(y = \beta_0 + \beta_1x + \epsilon\) involves finding the values of \(\beta_0\) and \(\beta_1\) that minimize the sum of squared residuals:

\[ S(\beta_0, \beta_1) = \sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1x_i))^2 \]

where \(y_i\) is the observed value, \(x_i\) is the independent variable, and \(n\) is the number of observations. The solution to this minimization problem involves taking the partial derivatives of \(S\) with respect to \(\beta_0\) and \(\beta_1\), setting them to zero, and solving the resulting equations.

Applications

Least squares is used in various fields for different purposes:

- In statistics, it is used for estimation and inference in linear models. - In geodesy and geophysics, least squares is used to process and analyze data. - In machine learning, it is employed in linear regression models to predict outcomes based on input variables. - In economics, it helps in estimating the relationships between variables.

Types of Least Squares

There are several variations of the least squares method, including:

- Ordinary Least Squares (OLS): The most common form, used when the errors are independently and identically distributed and there is no multicollinearity. - Weighted Least Squares (WLS): Used when the variances of the errors are not constant across observations. - Generalized Least Squares (GLS): Addresses situations where the error terms are correlated or have non-constant variance. - Non-Linear Least Squares: Used for fitting non-linear models to data.

Limitations

While the least squares method is powerful, it has limitations. It is sensitive to outliers and assumes that the errors are normally distributed and homoscedastic (having constant variance). When these assumptions are violated, alternative methods or adjustments may be necessary.

Conclusion

Least squares is a cornerstone technique in statistical analysis and data fitting, providing a foundation for understanding and modeling the relationships between variables. Its versatility and simplicity have made it a standard tool in numerous scientific and engineering disciplines.

This article is a stub. You can help WikiMD by registering to expand it. Editing is available only to registered and verified users. WikiMD is a comprehensive, free health & wellness encyclopedia.