Kurtosis


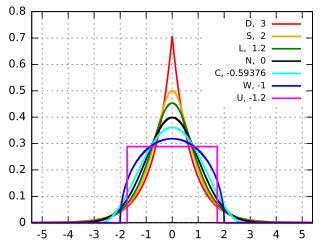
Kurtosis is a statistical measure that describes the shape of a probability distribution's tails in relation to its overall shape. The concept of kurtosis is an important aspect in the field of statistics, data analysis, and probability theory, providing insights into the distribution's tail heaviness or lightness compared to a normal distribution. Kurtosis is derived from a standardized moment of a distribution and can be used to identify the presence of outliers, assess risk, and test hypotheses.
Definition[edit]
Kurtosis is calculated as the fourth standardized moment of a distribution. The formula for kurtosis is given by:
\[ K = \frac{E[(X - \mu)^4]}{\sigma^4} \]
where \(E\) is the expectation, \(X\) is a random variable, \(\mu\) is the mean of \(X\), and \(\sigma\) is the standard deviation of \(X\). This formula calculates what is known as the "excess kurtosis," which subtracts 3 from the result to compare it directly against the normal distribution (which has a kurtosis of 3). Therefore, a distribution with a kurtosis less than 3 is considered "platykurtic," indicating it has lighter tails than a normal distribution. A kurtosis greater than 3 signifies a "leptokurtic" distribution, which has heavier tails. A kurtosis of exactly 3 defines a "mesokurtic" distribution, which is the normal distribution.
Types of Kurtosis[edit]
- Leptokurtic (Kurtosis > 3): Distributions that are leptokurtic exhibit tails that are fatter than those of a normal distribution, indicating a higher likelihood of extreme values (outliers).
- Platykurtic (Kurtosis < 3): In contrast, platykurtic distributions have thinner tails, suggesting a lower likelihood of extreme values.
- Mesokurtic (Kurtosis = 3): Mesokurtic distributions, including the normal distribution, have kurtosis values that indicate an average tail thickness.
Applications[edit]
Kurtosis is widely used in various fields such as finance, engineering, and psychology to analyze the behavior of data distributions, especially in the context of risk management and anomaly detection. In finance, for example, a higher kurtosis of asset returns may indicate a higher risk of investment due to the increased likelihood of extreme returns.
Interpretation[edit]
While kurtosis provides valuable information about the tail properties of a distribution, it is important to interpret its values in conjunction with other statistical measures such as skewness, mean, and standard deviation. Kurtosis alone does not give a complete picture of a distribution's shape, especially since it does not differentiate between the behavior of the tails and the peak of the distribution.
Limitations[edit]
One limitation of kurtosis is its sensitivity to sample size and outliers. Small changes in data can significantly affect the kurtosis value, making it sometimes unreliable for small datasets or those with pronounced outliers. Additionally, interpreting kurtosis can be challenging without a thorough understanding of the underlying data and its distribution.
Ad. Transform your life with W8MD's Budget GLP-1 injections from $75


W8MD offers a medical weight loss program to lose weight in Philadelphia. Our physician-supervised medical weight loss provides:
- Weight loss injections in NYC (generic and brand names):
- Zepbound / Mounjaro, Wegovy / Ozempic, Saxenda
- Most insurances accepted or discounted self-pay rates. We will obtain insurance prior authorizations if needed.
- Generic GLP1 weight loss injections from $75 for the starting dose.
- Also offer prescription weight loss medications including Phentermine, Qsymia, Diethylpropion, Contrave etc.
NYC weight loss doctor appointmentsNYC weight loss doctor appointments
Start your NYC weight loss journey today at our NYC medical weight loss and Philadelphia medical weight loss clinics.
- Call 718-946-5500 to lose weight in NYC or for medical weight loss in Philadelphia 215-676-2334.
- Tags:NYC medical weight loss, Philadelphia lose weight Zepbound NYC, Budget GLP1 weight loss injections, Wegovy Philadelphia, Wegovy NYC, Philadelphia medical weight loss, Brookly weight loss and Wegovy NYC
|
WikiMD's Wellness Encyclopedia |
| Let Food Be Thy Medicine Medicine Thy Food - Hippocrates |
Medical Disclaimer: WikiMD is not a substitute for professional medical advice. The information on WikiMD is provided as an information resource only, may be incorrect, outdated or misleading, and is not to be used or relied on for any diagnostic or treatment purposes. Please consult your health care provider before making any healthcare decisions or for guidance about a specific medical condition. WikiMD expressly disclaims responsibility, and shall have no liability, for any damages, loss, injury, or liability whatsoever suffered as a result of your reliance on the information contained in this site. By visiting this site you agree to the foregoing terms and conditions, which may from time to time be changed or supplemented by WikiMD. If you do not agree to the foregoing terms and conditions, you should not enter or use this site. See full disclaimer.
Credits:Most images are courtesy of Wikimedia commons, and templates, categories Wikipedia, licensed under CC BY SA or similar.
Translate this page: - East Asian
中文,
日本,
한국어,
South Asian
हिन्दी,
தமிழ்,
తెలుగు,
Urdu,
ಕನ್ನಡ,
Southeast Asian
Indonesian,
Vietnamese,
Thai,
မြန်မာဘာသာ,
বাংলা
European
español,
Deutsch,
français,
Greek,
português do Brasil,
polski,
română,
русский,
Nederlands,
norsk,
svenska,
suomi,
Italian
Middle Eastern & African
عربى,
Turkish,
Persian,
Hebrew,
Afrikaans,
isiZulu,
Kiswahili,
Other
Bulgarian,
Hungarian,
Czech,
Swedish,
മലയാളം,
मराठी,
ਪੰਜਾਬੀ,
ગુજરાતી,
Portuguese,
Ukrainian


