Bayesian inference

Bayes theorem visualisation

Bayesian inference event space

Bayesian inference archaeology example

Ebits2c

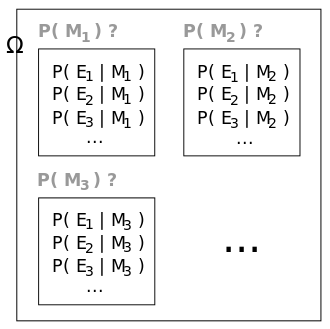
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics, that has applications in a wide range of disciplines, including engineering, biology, chemistry, and social sciences.

Overview

Bayesian inference derives its name from Thomas Bayes, who formulated a specific case of Bayes' theorem in his paper published posthumously in 1763. The general form of Bayes' theorem provides a way to update the probabilities of hypotheses based on observed evidence. In the context of Bayesian inference, the probability of a hypothesis before observing the evidence is known as the prior probability. The probability of observing the evidence given that the hypothesis is true is known as the likelihood. The updated probability of the hypothesis after observing the evidence is known as the posterior probability.

Mathematical Formulation

The mathematical formulation of Bayesian inference involves calculating the posterior probability according to Bayes' theorem. The theorem is expressed as:

\[ P(H|E) = \frac{P(E|H) \cdot P(H)}{P(E)} \]

where:

• \(P(H|E)\) is the posterior probability of the hypothesis \(H\) given the evidence \(E\),
• \(P(E|H)\) is the likelihood of observing evidence \(E\) given that hypothesis \(H\) is true,
• \(P(H)\) is the prior probability of hypothesis \(H\), and
• \(P(E)\) is the probability of observing the evidence.

Applications

Bayesian inference has a wide range of applications across various fields. In medicine, it is used for disease screening and for making decisions based on patient data. In machine learning, Bayesian methods are employed in the development of spam filters and in the creation of algorithms that can learn from data. In environmental science, Bayesian inference is used for modeling climate change and assessing the impact of human activities on the environment.

Advantages and Disadvantages

One of the main advantages of Bayesian inference is its flexibility in incorporating prior knowledge about a system or phenomenon. This can be particularly useful in situations where data is limited or expensive to obtain. However, a significant disadvantage is the subjective nature of choosing a prior, which can lead to different conclusions based on different priors.

Conclusion

Bayesian inference is a powerful and versatile method for statistical analysis that allows for the incorporation of prior knowledge and the updating of probabilities with new evidence. Its applications span a wide range of fields, demonstrating its utility in solving complex problems.

This article is a medical stub. You can help WikiMD by expanding it!
Most recent articles Ongoing trials	Wikipedia