Scaled inverse chi-squared distribution: Difference between revisions
CSV import |
CSV import |
||
| Line 45: | Line 45: | ||
{{Statistics-stub}} | {{Statistics-stub}} | ||
<gallery> | |||
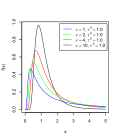
File:Scaled inverse chi squared.svg|Scaled inverse chi squared | |||
File:Scaled inverse chi squared cdf.svg|Scaled inverse chi squared cdf | |||
</gallery> | |||
Latest revision as of 05:35, 3 March 2025
Scaled Inverse Chi-Squared Distribution
The Scaled Inverse Chi-Squared Distribution is a probability distribution that is widely used in Bayesian statistics, particularly in the context of Bayesian inference and hierarchical models. It is a two-parameter family of continuous probability distributions and is closely related to the Inverse chi-squared distribution and the Inverse gamma distribution.
Definition[edit]
The scaled inverse chi-squared distribution is defined by two parameters: the degrees of freedom \( \nu > 0 \) and the scale parameter \( \sigma^2 > 0 \). The probability density function (pdf) of the scaled inverse chi-squared distribution for \( x > 0 \) is given by:
\[ f(x|\nu,\sigma^2) = \frac{(\frac{\nu\sigma^2}{2})^{\frac{\nu}{2}}}{\Gamma(\frac{\nu}{2})} x^{-\frac{\nu}{2}-1} \exp\left(-\frac{\nu\sigma^2}{2x}\right) \]
where \( \Gamma \) is the Gamma function.
Properties[edit]
Mean[edit]
If \( \nu > 2 \), the mean of the scaled inverse chi-squared distribution is:
\[ \text{Mean} = \frac{\nu\sigma^2}{\nu-2} \]
Variance[edit]
If \( \nu > 4 \), the variance is:
\[ \text{Variance} = \frac{2(\nu\sigma^2)^2}{(\nu-2)^2(\nu-4)} \]
Mode[edit]
The mode of the distribution is:
\[ \text{Mode} = \frac{\nu\sigma^2}{\nu+2} \]
Applications[edit]
The scaled inverse chi-squared distribution is particularly useful in Bayesian statistics as a Conjugate prior for the variance of a normally distributed population when the mean is known. It is also used in the Bayesian analysis of variance (ANOVA) models and in the estimation of random effects in hierarchical linear models.
Related Distributions[edit]
- The Inverse chi-squared distribution is a special case of the scaled inverse chi-squared distribution with \( \sigma^2 = 1 \). - The Inverse gamma distribution is a generalization of the scaled inverse chi-squared distribution. - When the scale parameter \( \sigma^2 \) is known, the scaled inverse chi-squared distribution is related to the Chi-squared distribution through a transformation.
See Also[edit]

This article is a statistics-related stub. You can help WikiMD by expanding it!
-
Scaled inverse chi squared
-
Scaled inverse chi squared cdf