Conditional probability: Difference between revisions
CSV import Tags: mobile edit mobile web edit |
CSV import Tags: mobile edit mobile web edit |
||
| Line 32: | Line 32: | ||
{{dictionary-stub1}} | {{dictionary-stub1}} | ||
{{dictionary-stub1}} | {{dictionary-stub1}} | ||
<gallery> | |||
File:Conditional_probability.svg|Conditional probability | |||
File:Probability_tree_diagram.svg|Probability tree diagram | |||
File:Venn_Pie_Chart_describing_Bayes'_law.png|Venn Pie Chart describing Bayes' law | |||
File:Bayes_theorem_visualisation.svg|Bayes theorem visualisation | |||
</gallery> | |||
Latest revision as of 04:58, 18 February 2025
Conditional probability is a concept in probability theory that calculates the probability of an event given the occurrence of another event. It is a fundamental concept in statistics and data analysis, and is used in a variety of fields, including medicine, psychology, and economics.
Definition[edit]
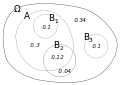
In probability theory, the conditional probability of an event B is the probability that the event will occur given the knowledge that an event A has already occurred. This is usually expressed as P(B|A), which reads as "the probability of B given A".
Calculation[edit]
The calculation of conditional probability is based on the formula:
P(B|A) = P(A ∩ B) / P(A)
where:
- P(A ∩ B) is the probability of both events A and B occurring
- P(A) is the probability of event A occurring
Applications[edit]
Conditional probability has a wide range of applications in various fields. In medicine, it is used in epidemiology to determine the likelihood of a disease given a certain condition or exposure. In psychology, it is used in behavioral studies to predict behavior based on past actions. In economics, it is used in risk assessment and decision making.
See also[edit]
References[edit]
<references />