Root mean square
Root mean square (RMS) is a statistical measure that is commonly used in various fields to quantify the average magnitude of a set of values. It is particularly useful in analyzing data that fluctuates over time, such as electrical signals or sound waves. The RMS value provides a way to express the overall "size" or "amplitude" of the data set, taking into account both positive and negative values.
Definition[edit]
The root mean square is calculated by taking the square root of the mean of the squared values in a data set. Mathematically, it can be expressed as:
{{{1}}} }
where n is the number of values in the data set, and x_i represents each individual value.
Applications[edit]
Electrical Engineering[edit]
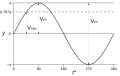
In electrical engineering, the RMS value is commonly used to measure the voltage or current of an alternating current (AC) signal. Since AC signals continuously change their polarity, simply taking the average value would not accurately represent the signal's magnitude. By calculating the RMS value, engineers can determine the effective voltage or current that would produce the same amount of power in a direct current (DC) circuit.
Audio Engineering[edit]
In audio engineering, the RMS value is used to measure the amplitude of sound waves. By calculating the RMS value of an audio signal, engineers can determine the average power or loudness of the sound. This information is crucial in various applications, such as audio recording, mixing, and mastering.
Statistics[edit]
In statistics, the RMS value is often used as a measure of dispersion or variability within a data set. It provides a way to quantify the spread of values around the mean. By comparing the RMS values of different data sets, statisticians can assess the relative variability and make informed decisions based on the data.
Advantages[edit]
The use of RMS has several advantages in various fields:
- Symmetry - The RMS value takes into account both positive and negative values, making it suitable for analyzing data with alternating polarity.
- Meaningful representation - Unlike the average value, which can be influenced by extreme outliers, the RMS value provides a more representative measure of the overall magnitude of the data set.
- Compatibility - The RMS value can be easily compared and combined with other statistical measures, such as standard deviation or variance, to gain a more comprehensive understanding of the data.
Limitations[edit]
While the RMS value is a useful measure, it is important to be aware of its limitations:
- Non-linearity - The RMS value assumes that the data set follows a linear relationship. In cases where the data exhibits non-linear behavior, alternative measures may be more appropriate.
- Context-dependency - The interpretation of the RMS value depends on the specific application and context. It is essential to consider the domain-specific requirements and limitations when using RMS as a measure.
See Also[edit]
References[edit]
<references />
-
Waveforms
-
Dutycycle
-
Sine wave voltages
Ad. Transform your life with W8MD's Budget GLP-1 injections from $75


W8MD offers a medical weight loss program to lose weight in Philadelphia. Our physician-supervised medical weight loss provides:
- Weight loss injections in NYC (generic and brand names):
- Zepbound / Mounjaro, Wegovy / Ozempic, Saxenda
- Most insurances accepted or discounted self-pay rates. We will obtain insurance prior authorizations if needed.
- Generic GLP1 weight loss injections from $75 for the starting dose.
- Also offer prescription weight loss medications including Phentermine, Qsymia, Diethylpropion, Contrave etc.
NYC weight loss doctor appointmentsNYC weight loss doctor appointments
Start your NYC weight loss journey today at our NYC medical weight loss and Philadelphia medical weight loss clinics.
- Call 718-946-5500 to lose weight in NYC or for medical weight loss in Philadelphia 215-676-2334.
- Tags:NYC medical weight loss, Philadelphia lose weight Zepbound NYC, Budget GLP1 weight loss injections, Wegovy Philadelphia, Wegovy NYC, Philadelphia medical weight loss, Brookly weight loss and Wegovy NYC
|
WikiMD's Wellness Encyclopedia |
| Let Food Be Thy Medicine Medicine Thy Food - Hippocrates |
Medical Disclaimer: WikiMD is not a substitute for professional medical advice. The information on WikiMD is provided as an information resource only, may be incorrect, outdated or misleading, and is not to be used or relied on for any diagnostic or treatment purposes. Please consult your health care provider before making any healthcare decisions or for guidance about a specific medical condition. WikiMD expressly disclaims responsibility, and shall have no liability, for any damages, loss, injury, or liability whatsoever suffered as a result of your reliance on the information contained in this site. By visiting this site you agree to the foregoing terms and conditions, which may from time to time be changed or supplemented by WikiMD. If you do not agree to the foregoing terms and conditions, you should not enter or use this site. See full disclaimer.
Credits:Most images are courtesy of Wikimedia commons, and templates, categories Wikipedia, licensed under CC BY SA or similar.
Translate this page: - East Asian
中文,
日本,
한국어,
South Asian
हिन्दी,
தமிழ்,
తెలుగు,
Urdu,
ಕನ್ನಡ,
Southeast Asian
Indonesian,
Vietnamese,
Thai,
မြန်မာဘာသာ,
বাংলা
European
español,
Deutsch,
français,
Greek,
português do Brasil,
polski,
română,
русский,
Nederlands,
norsk,
svenska,
suomi,
Italian
Middle Eastern & African
عربى,
Turkish,
Persian,
Hebrew,
Afrikaans,
isiZulu,
Kiswahili,
Other
Bulgarian,
Hungarian,
Czech,
Swedish,
മലയാളം,
मराठी,
ਪੰਜਾਬੀ,
ગુજરાતી,
Portuguese,
Ukrainian