Harmonic oscillator

Harmonic Oscillator

The harmonic oscillator is a fundamental concept within physics, describing a system that, when displaced from its equilibrium position, experiences a restoring force, F, directly proportional to the displacement, x, according to Hooke's Law: F = -kx, where k is a positive constant. This principle applies to a variety of physical systems, including mechanical oscillators like springs and pendulums, as well as electrical circuits and quantum mechanics scenarios.

Overview

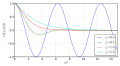
A harmonic oscillator can be classified as either a simple or damped oscillator, depending on whether it loses energy to its surroundings. In the absence of damping and external forces, a simple harmonic oscillator will oscillate indefinitely with a specific natural frequency, ω₀, which depends on the mass of the system and the force constant, k. The motion of a simple harmonic oscillator is described by the equation x(t) = A cos(ω₀t + φ), where A is the amplitude, ω₀ is the angular frequency, and φ is the phase constant.

Damped Harmonic Oscillator

In real-world applications, oscillating systems often experience damping, which gradually reduces the amplitude of oscillation due to non-conservative forces such as friction or air resistance. The equation of motion for a damped harmonic oscillator is modified to include a damping term, proportional to the velocity, -bẋ, leading to the equation ẍ + (b/m)ẋ + (k/m)x = 0, where b is the damping coefficient, m is the mass, and k is the spring constant. Depending on the value of b, the system may exhibit underdamped, critically damped, or overdamped behavior.

Forced Harmonic Oscillator

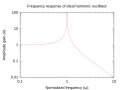
A forced harmonic oscillator is subject to an external periodic force, F(t) = F₀ cos(ωt), where F₀ is the amplitude of the force and ω is its angular frequency. This leads to complex behavior, including resonance when the driving frequency matches the natural frequency of the system, resulting in a significant increase in the amplitude of oscillation.

Quantum Harmonic Oscillator

In quantum mechanics, the harmonic oscillator model is used to describe the behavior of particles in potential wells, with energy levels quantized into discrete values. The Schrödinger equation for a quantum harmonic oscillator reveals that the energy levels are given by E_n = (n + 1/2)ħω₀, where n is a non-negative integer, ħ is the reduced Planck constant, and ω₀ is the angular frequency of the oscillator.

Applications

Harmonic oscillators are ubiquitous in physics and engineering, modeling systems ranging from molecular vibrations and atomic lattice structures in solid-state physics to the design of buildings for earthquake resistance. In electronics, LC circuits behave as harmonic oscillators, forming the basis of oscillators and filters in radio and television transmitters and receivers.

See Also

• Simple harmonic motion
• Damping
• Resonance
• Quantum mechanics
• LC circuit

   This article is a physics-related stub. You can help WikiMD by expanding it!

Harmonic oscillator gallery

• 

  Animated mass spring faster

• 

  Simple harmonic motion animation

• 

  Damping 1

• 

  Step response for two-pole feedback amplifier

• 

  Mplwp resonance zeta envelope

• 

  Harmonic oscillator gain

• 

  Simple pendulum height

• 

  Harmonic oscillator