Fast Fourier transform
Fast Fourier Transform[edit]
The Fast Fourier Transform (FFT) is an efficient algorithm used to compute the Discrete Fourier Transform (DFT) of a sequence or signal. It is widely used in various fields, including signal processing, image processing, audio compression, and data analysis. The FFT algorithm was developed by Cooley and Tukey in 1965 and has since become one of the most important algorithms in modern computing.
History[edit]
The concept of the Fourier Transform was introduced by Jean-Baptiste Joseph Fourier in the early 19th century. Fourier's idea was to represent a function as a sum of sinusoidal functions with different frequencies. However, computing the Fourier Transform directly using the definition was computationally expensive, especially for large datasets.
In the 1960s, James Cooley and John Tukey developed the Fast Fourier Transform algorithm, which significantly reduced the computational complexity of the Fourier Transform. The FFT algorithm exploits the symmetry properties of the Fourier Transform to reduce the number of computations required. This breakthrough made the Fourier Transform practical for real-time applications and revolutionized the field of signal processing.
Algorithm[edit]
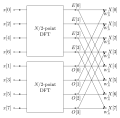
The FFT algorithm is based on the divide-and-conquer strategy. It recursively divides the input sequence into smaller subsequences and computes the DFT of each subsequence. The DFT of the original sequence is then obtained by combining the DFTs of the smaller subsequences.
The key insight of the FFT algorithm is that the DFT of a sequence of length N can be expressed in terms of the DFTs of two sequences of length N/2. This property allows the algorithm to reduce the number of computations from O(N^2) to O(N log N), making it much more efficient for large datasets.
The FFT algorithm can be implemented using various techniques, such as the Cooley-Tukey algorithm, the Radix-2 algorithm, or the Split-Radix algorithm. These techniques differ in the way they divide the input sequence and combine the DFTs of the smaller subsequences.
Applications[edit]
The Fast Fourier Transform has numerous applications in various fields:
- **Signal Processing**: The FFT is widely used for analyzing and processing signals in fields such as telecommunications, audio processing, and image processing. It allows for efficient filtering, noise reduction, and spectral analysis of signals.
- **Image Processing**: The FFT is used in image processing for tasks such as image enhancement, image compression, and image recognition. It enables the transformation of images between the spatial domain and the frequency domain, allowing for efficient manipulation of image data.
- **Audio Compression**: The FFT is a fundamental component of audio compression algorithms, such as MP3 and AAC. It is used to convert audio signals into the frequency domain, where compression techniques can be applied to reduce the amount of data required for storage or transmission.
- **Data Analysis**: The FFT is used in data analysis to extract meaningful information from time series data. It is commonly used in fields such as finance, physics, and engineering for tasks such as spectral analysis, correlation analysis, and pattern recognition.
See Also[edit]
- Discrete Fourier Transform: The mathematical concept on which the Fast Fourier Transform is based. - Cooley-Tukey algorithm: The specific algorithm developed by Cooley and Tukey for computing the FFT. - Radix-2 algorithm: Another popular algorithm for computing the FFT. - Split-Radix algorithm: A variant of the Radix-2 algorithm that further reduces the computational complexity.
References[edit]
1. Cooley, J. W., & Tukey, J. W. (1965). An algorithm for the machine calculation of complex Fourier series. Mathematics of Computation, 19(90), 297-301.
2. Bracewell, R. N. (1986). The Fourier Transform and Its Applications. McGraw-Hill.
3. Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing. Pearson Education.
-
Butterfly diagram of the Decimation in Time FFT algorithm
-
FFT of a cosine summation function
-
Comparison of time domain and frequency domain
Ad. Transform your life with W8MD's Budget GLP-1 injections from $75


W8MD offers a medical weight loss program to lose weight in Philadelphia. Our physician-supervised medical weight loss provides:
- Weight loss injections in NYC (generic and brand names):
- Zepbound / Mounjaro, Wegovy / Ozempic, Saxenda
- Most insurances accepted or discounted self-pay rates. We will obtain insurance prior authorizations if needed.
- Generic GLP1 weight loss injections from $75 for the starting dose.
- Also offer prescription weight loss medications including Phentermine, Qsymia, Diethylpropion, Contrave etc.
NYC weight loss doctor appointmentsNYC weight loss doctor appointments
Start your NYC weight loss journey today at our NYC medical weight loss and Philadelphia medical weight loss clinics.
- Call 718-946-5500 to lose weight in NYC or for medical weight loss in Philadelphia 215-676-2334.
- Tags:NYC medical weight loss, Philadelphia lose weight Zepbound NYC, Budget GLP1 weight loss injections, Wegovy Philadelphia, Wegovy NYC, Philadelphia medical weight loss, Brookly weight loss and Wegovy NYC
|
WikiMD's Wellness Encyclopedia |
| Let Food Be Thy Medicine Medicine Thy Food - Hippocrates |
Medical Disclaimer: WikiMD is not a substitute for professional medical advice. The information on WikiMD is provided as an information resource only, may be incorrect, outdated or misleading, and is not to be used or relied on for any diagnostic or treatment purposes. Please consult your health care provider before making any healthcare decisions or for guidance about a specific medical condition. WikiMD expressly disclaims responsibility, and shall have no liability, for any damages, loss, injury, or liability whatsoever suffered as a result of your reliance on the information contained in this site. By visiting this site you agree to the foregoing terms and conditions, which may from time to time be changed or supplemented by WikiMD. If you do not agree to the foregoing terms and conditions, you should not enter or use this site. See full disclaimer.
Credits:Most images are courtesy of Wikimedia commons, and templates, categories Wikipedia, licensed under CC BY SA or similar.
Translate this page: - East Asian
中文,
日本,
한국어,
South Asian
हिन्दी,
தமிழ்,
తెలుగు,
Urdu,
ಕನ್ನಡ,
Southeast Asian
Indonesian,
Vietnamese,
Thai,
မြန်မာဘာသာ,
বাংলা
European
español,
Deutsch,
français,
Greek,
português do Brasil,
polski,
română,
русский,
Nederlands,
norsk,
svenska,
suomi,
Italian
Middle Eastern & African
عربى,
Turkish,
Persian,
Hebrew,
Afrikaans,
isiZulu,
Kiswahili,
Other
Bulgarian,
Hungarian,
Czech,
Swedish,
മലയാളം,
मराठी,
ਪੰਜਾਬੀ,
ગુજરાતી,
Portuguese,
Ukrainian