Euclidean vector: Difference between revisions
CSV import Tags: mobile edit mobile web edit |
CSV import |
||
| Line 32: | Line 32: | ||
{{math-stub}} | {{math-stub}} | ||
== Euclidean vector gallery == | |||
<gallery> | |||
File:Vector from A to B.svg|Vector from A to B | |||
File:vector from A to B.svg|Vector from A to B | |||
File:Notation for vectors in or out of a plane.svg|Notation for vectors in or out of a plane | |||
File:Position vector.svg|Position vector | |||
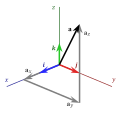
File:3D Vector.svg|3D Vector | |||
File:Surface normal tangent.svg|Surface normal tangent | |||
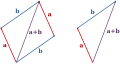
File:Vector addition.svg|Vector addition | |||
File:Vector subtraction.svg|Vector subtraction | |||
File:Scalar multiplication by r=3.svg|Scalar multiplication by r=3 | |||
File:Scalar multiplication of vectors2.svg|Scalar multiplication of vectors | |||
</gallery> | |||
Latest revision as of 05:37, 3 March 2025
Euclidean vector
A Euclidean vector (also known as a geometric vector or simply a vector) is a geometric object that possesses both a magnitude and a direction. A vector can be represented as an arrow pointing from one point to another in a Euclidean space. The length of the arrow represents the vector's magnitude, while the direction in which the arrow points represents the vector's direction.
Definition[edit]
In mathematics, particularly in linear algebra and physics, a Euclidean vector is typically represented in a Cartesian coordinate system by ordered pairs or triples of real numbers. These numbers denote the vector's components along the Cartesian axes. For example, in a three-dimensional space, a vector can be represented as (x, y, z), where x, y, and z are the components of the vector.
Properties[edit]
Euclidean vectors have several important properties that make them fundamental in the study of linear algebra and physics. These include:
- Addition: Two vectors can be added together to form a new vector, known as the resultant vector, which is obtained by placing the tail of the second vector at the head of the first vector and then drawing a vector from the tail of the first vector to the head of the second vector.
- Scalar multiplication: A vector can be multiplied by a scalar (a real number), resulting in a new vector whose magnitude is scaled by the absolute value of the scalar, and whose direction is the same as the original vector if the scalar is positive, and opposite if the scalar is negative.
- Dot product: Also known as the scalar product, the dot product of two vectors is a scalar that reflects the degree of parallelism between the vectors.
- Cross product: In three-dimensional space, the cross product of two vectors is a vector that is perpendicular to the plane containing the two vectors, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
Applications[edit]
Euclidean vectors are used in various scientific fields, including physics, engineering, computer science, and mathematics, due to their ability to succinctly represent points, directions, and velocities. In physics, vectors are used to describe quantities that have both magnitude and direction, such as force, velocity, and acceleration. In computer graphics, vectors are used to represent the positions and orientations of objects in a virtual space.
See also[edit]
References[edit]
<references/>

This article is a mathematics-related stub. You can help WikiMD by expanding it!
Euclidean vector gallery[edit]
-
Vector from A to B
-
Vector from A to B
-
Notation for vectors in or out of a plane
-
Position vector
-
3D Vector
-
Surface normal tangent
-
Vector addition
-
Vector subtraction
-
Scalar multiplication by r=3
-
Scalar multiplication of vectors