Inverse transform sampling

Inverse Transform Sampling (ITS), also known as the inverse probability integral transform, is a fundamental method in the field of statistics and probability theory for generating sample numbers at random from any probability distribution, given its cumulative distribution function (CDF). This technique is widely used in simulation and Monte Carlo methods, where it allows for the transformation of uniformly distributed random numbers into numbers distributed according to a desired distribution.

Overview

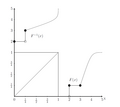
The principle behind inverse transform sampling is based on the properties of the cumulative distribution function. For a given continuous random variable X with a probability density function (PDF) f(x) and a cumulative distribution function F(x), the CDF is defined as:

F(x) = P(X \leq x) = \int_{-\infty}^{x} f(t) dt

The CDF F(x) is a non-decreasing function that ranges from 0 to 1. The inverse transform sampling method exploits the fact that if U is a uniform random variable on the interval [0, 1], then the variable X defined as F^(-1)(U) has the same distribution as the original variable with CDF F(x).

Procedure

The steps involved in inverse transform sampling are as follows:

1. Generate a random number u from the uniform distribution over the interval [0, 1].
2. Compute the inverse of the cumulative distribution function, F^(-1)(u).
3. The value obtained in step 2 is a random number that follows the desired distribution.

Applications

Inverse transform sampling is utilized in various fields such as computer science, engineering, and finance, where simulations involving random variables are required. It is particularly useful in cases where direct sampling from the desired distribution is complex or infeasible.

Limitations

While inverse transform sampling is a powerful tool, it has limitations. The method requires the inverse of the CDF to be known or easily computable, which is not always the case. For distributions where the inverse CDF is difficult to obtain, alternative methods such as rejection sampling, Markov chain Monte Carlo methods, or piecewise linear approximation may be more appropriate.

See Also

• Monte Carlo method
• Probability distribution
• Cumulative distribution function
• Rejection sampling
• Markov chain Monte Carlo

References

<references/>

   This article is a statistics-related stub. You can help WikiMD by expanding it!

• 
  Inverse transform sampling
• 
  Inverse function
• 
  Generalized inversion method
• 
  Inverse transform sampling example
• 
  Inverse transformation method for exponential distribution