Fast Fourier transform

Fast Fourier Transform

The Fast Fourier Transform (FFT) is an efficient algorithm used to compute the Discrete Fourier Transform (DFT) of a sequence or signal. It is widely used in various fields, including signal processing, image processing, audio compression, and data analysis. The FFT algorithm was developed by Cooley and Tukey in 1965 and has since become one of the most important algorithms in modern computing.

History

The concept of the Fourier Transform was introduced by Jean-Baptiste Joseph Fourier in the early 19th century. Fourier's idea was to represent a function as a sum of sinusoidal functions with different frequencies. However, computing the Fourier Transform directly using the definition was computationally expensive, especially for large datasets.

In the 1960s, James Cooley and John Tukey developed the Fast Fourier Transform algorithm, which significantly reduced the computational complexity of the Fourier Transform. The FFT algorithm exploits the symmetry properties of the Fourier Transform to reduce the number of computations required. This breakthrough made the Fourier Transform practical for real-time applications and revolutionized the field of signal processing.

Algorithm

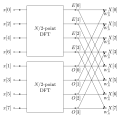
The FFT algorithm is based on the divide-and-conquer strategy. It recursively divides the input sequence into smaller subsequences and computes the DFT of each subsequence. The DFT of the original sequence is then obtained by combining the DFTs of the smaller subsequences.

The key insight of the FFT algorithm is that the DFT of a sequence of length N can be expressed in terms of the DFTs of two sequences of length N/2. This property allows the algorithm to reduce the number of computations from O(N^2) to O(N log N), making it much more efficient for large datasets.

The FFT algorithm can be implemented using various techniques, such as the Cooley-Tukey algorithm, the Radix-2 algorithm, or the Split-Radix algorithm. These techniques differ in the way they divide the input sequence and combine the DFTs of the smaller subsequences.

Applications

The Fast Fourier Transform has numerous applications in various fields:

- **Signal Processing**: The FFT is widely used for analyzing and processing signals in fields such as telecommunications, audio processing, and image processing. It allows for efficient filtering, noise reduction, and spectral analysis of signals.

- **Image Processing**: The FFT is used in image processing for tasks such as image enhancement, image compression, and image recognition. It enables the transformation of images between the spatial domain and the frequency domain, allowing for efficient manipulation of image data.

- **Audio Compression**: The FFT is a fundamental component of audio compression algorithms, such as MP3 and AAC. It is used to convert audio signals into the frequency domain, where compression techniques can be applied to reduce the amount of data required for storage or transmission.

- **Data Analysis**: The FFT is used in data analysis to extract meaningful information from time series data. It is commonly used in fields such as finance, physics, and engineering for tasks such as spectral analysis, correlation analysis, and pattern recognition.

See Also

- Discrete Fourier Transform: The mathematical concept on which the Fast Fourier Transform is based. - Cooley-Tukey algorithm: The specific algorithm developed by Cooley and Tukey for computing the FFT. - Radix-2 algorithm: Another popular algorithm for computing the FFT. - Split-Radix algorithm: A variant of the Radix-2 algorithm that further reduces the computational complexity.

References

1. Cooley, J. W., & Tukey, J. W. (1965). An algorithm for the machine calculation of complex Fourier series. Mathematics of Computation, 19(90), 297-301.

2. Bracewell, R. N. (1986). The Fourier Transform and Its Applications. McGraw-Hill.

3. Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing. Pearson Education.

• 
  Butterfly diagram of the Decimation in Time FFT algorithm
• 
  FFT of a cosine summation function
• 
  Comparison of time domain and frequency domain