Gamma function: Difference between revisions
CSV import Tags: mobile edit mobile web edit |
CSV import |
||
| Line 46: | Line 46: | ||
{{math-stub}} | {{math-stub}} | ||
<gallery> | |||
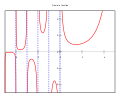
File:Gamma plot.svg|Gamma plot | |||
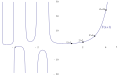
File:Generalized factorial function more infos.svg|Generalized factorial function more infos | |||
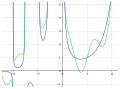
File:Gamma plus sin pi z.svg|Gamma plus sin pi z | |||
File:Plot of gamma function in complex plane in 3D with color and legend and 1000 plot points created with Mathematica.svg|Plot of gamma function in complex plane in 3D with color and legend and 1000 plot points created with Mathematica | |||
File:Plot of gamma function in the complex plane from -2-i to 6+2i with colors created in Mathematica.svg|Plot of gamma function in the complex plane from -2-i to 6+2i with colors created in Mathematica | |||
File:Gamma cplot.svg|Gamma cplot | |||
File:Gamma abs 3D.png|Gamma abs 3D | |||
File:LogGamma Analytic Function.png|LogGamma Analytic Function | |||
File:Plot of logarithmic gamma function in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D.svg|Plot of logarithmic gamma function in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D | |||
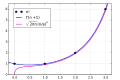
File:Mplwp factorial gamma stirling.svg|Mplwp factorial gamma stirling | |||
</gallery> | |||
Latest revision as of 06:16, 3 March 2025

The Gamma function (denoted as \(\Gamma(n)\)) is a complex mathematical function that extends the concept of factorial to complex and real number arguments. It is used in various areas of mathematics, including calculus, statistics, and number theory, as well as in the fields of physics and engineering.
Definition[edit]
The Gamma function is defined for all complex numbers except the non-positive integers. For any positive integer \(n\), the Gamma function is given by:
\[ \Gamma(n) = (n-1)! \]
For complex numbers with a real part greater than 0, it is defined through an improper integral:
\[ \Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt \]
Properties[edit]
The Gamma function has several important properties:
- **Recurrence Relation**: \(\Gamma(z+1) = z\Gamma(z)\). This property helps in computing the Gamma function for any argument based on its value at another point.
- **Reflection Formula**: \(\Gamma(1-z)\Gamma(z) = \frac{\pi}{\sin(\pi z)}\). This formula is useful for evaluating the Gamma function for negative arguments.
- **Euler's Reflection Formula**: Provides a way to extend the Gamma function to complex numbers with a negative real part.
- **Multiplication Theorem**: A formula that relates the Gamma function at multiple points to a product of Gamma functions at those points, scaled by a power of 2 and \(\pi\).
Applications[edit]
The Gamma function is used in various branches of mathematics and science:
- In statistics, it is used to define the gamma distribution, a two-parameter family of continuous probability distributions.
- In physics, the Gamma function appears in the solutions of certain types of differential equations and in the calculation of partition functions.
- In number theory, it is involved in the study of Riemann zeta function and other L-functions.
Special Values[edit]
Some special values of the Gamma function include:
- \(\Gamma(\frac{1}{2}) = \sqrt{\pi}\), which is related to the Gaussian integral.
- \(\Gamma(1) = 0!\) and \(\Gamma(2) = 1!\), which align with the factorial function for positive integers.
See Also[edit]

This article is a mathematics-related stub. You can help WikiMD by expanding it!
-
Gamma plot
-
Generalized factorial function more infos
-
Gamma plus sin pi z
-
Plot of gamma function in complex plane in 3D with color and legend and 1000 plot points created with Mathematica
-
Plot of gamma function in the complex plane from -2-i to 6+2i with colors created in Mathematica
-
Gamma cplot
-
Gamma abs 3D
-
LogGamma Analytic Function
-
Plot of logarithmic gamma function in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Mplwp factorial gamma stirling