Linear regression: Difference between revisions
From WikiMD's Wellness Encyclopedia
CSV import |
CSV import |
||
| Line 48: | Line 48: | ||
{{stub}} | {{stub}} | ||
{{dictionary-stub1}} | {{dictionary-stub1}} | ||
<gallery> | |||
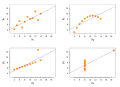
File:Linear_least_squares_example2.svg|Linear least squares example | |||
File:Polyreg_scheffe.svg|Polynomial regression example | |||
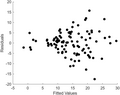
File:Heteroscedasticity_in_Linear_Regression.png|Heteroscedasticity in linear regression | |||
File:Independence_of_Errors_Assumption_for_Linear_Regressions.png|Independence of errors assumption for linear regressions | |||
File:Anscombe's_quartet_3.svg|Anscombe's quartet example | |||
File:Linear_regression.svg|Linear regression | |||
File:Galton's_correlation_diagram_1875.jpg|Galton's correlation diagram 1875 | |||
File:Thiel-Sen_estimator.svg|Thiel-Sen estimator | |||
</gallery> | |||
Latest revision as of 11:37, 18 February 2025
Linear regression is a statistical analysis technique used to understand the relationship between two variables. It is a fundamental tool in statistics, machine learning, and data science.
Overview[edit]
Linear regression models the relationship between two variables by fitting a linear equation to observed data. The steps to perform linear regression are:
- Collect and prepare data
- Choose the type of regression to use
- Create the model
- Check the model fit
- Make predictions
Types of Linear Regression[edit]
There are two types of linear regression:
- Simple linear regression: One independent variable and one dependent variable
- Multiple linear regression: More than one independent variable and one dependent variable
Assumptions of Linear Regression[edit]
Linear regression makes several assumptions:
- Linearity: The relationship between the independent and dependent variable is linear.
- Independence: The observations are independent of each other.
- Homoscedasticity: The variance of the errors is constant across all levels of the independent variables.
- Normality: The errors of the prediction will follow a normal distribution.
Applications of Linear Regression[edit]
Linear regression is used in various fields including:
- Economics: To understand the economic factors affecting business
- Finance: To predict stock prices
- Healthcare: To predict disease trends
- Machine Learning: As a prediction algorithm
See Also[edit]
|
|
|
-
Linear least squares example
-
Polynomial regression example
-
Heteroscedasticity in linear regression
-
Independence of errors assumption for linear regressions
-
Anscombe's quartet example
-
Linear regression
-
Galton's correlation diagram 1875
-
Thiel-Sen estimator