Interpolation

Interpolation is a method of constructing new data points within the range of a discrete set of known data points. It is widely used in many fields including mathematics, physics, and computer graphics.

Overview

In the mathematical field, interpolation is a type of estimation, a method of constructing new data points within the range of a discrete set of known data points. The primary function of interpolation in mathematics is to estimate values that fall between two known values.

In computer graphics, interpolation is used to produce a smooth gradient or to resize digital images. In the realm of physics, it is used to predict values for an element based on the known values of surrounding elements.

Types of Interpolation

There are several types of interpolation methods, including:

• Linear Interpolation - This is the simplest method of interpolation. In this method, two points are connected by a straight line and the value of an intermediate point is estimated using this line.

• Polynomial Interpolation - This is a more general form of interpolation which involves fitting a polynomial that passes through given points.

• Spline Interpolation - This method involves fitting a special type of piecewise polynomial called a spline to the data points.

• Rational Interpolation - This is a type of interpolation where the interpolant is a rational function.

Applications

Interpolation has a wide range of applications in various fields. Some of the notable applications include:

• Image Processing - Interpolation is used in image processing to increase the size of an image or to correct distortions.

• Computer Graphics - In computer graphics, interpolation is used to create smooth transitions between points and lines.

• Numerical Analysis - Interpolation is used in numerical analysis to solve differential equations and to approximate functions.

• Geostatistics - In geostatistics, interpolation is used to predict unknown values for any geographic location, based on the values at surrounding locations.

See Also

• Extrapolation
• Curve Fitting
• Regression Analysis

References

<references />

This article is a medical stub. You can help WikiMD by expanding it!
Most recent articles Ongoing trials	Wikipedia

• 
  Splined epitrochoid
• 
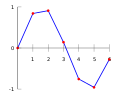
  Interpolation data
• 
  Piecewise constant interpolation
• 
  Linear interpolation example
• 
  Polynomial interpolation example
• 
  Spline interpolation example
• 
  Nearest 2D interpolation example
• 
  Bilinear interpolation example
• 
  Bicubic interpolation example