{{Short description|The reduction in fluid pressure that results when a fluid flows through a constricted section of a pipe.}}
{{Short description|The reduction in fluid pressure that results when a fluid flows through a constricted section of a pipe.}}
{{Use dmy dates|date=October 2023}}
==Venturi effect==
The '''Venturi effect''' is a phenomenon in fluid dynamics where a fluid's velocity increases and its pressure decreases as it flows through a constricted section of a pipe or channel. This effect is named after the Italian physicist [[Giovanni Battista Venturi]], who first observed it in the 18th century.
The '''Venturi effect''' is a phenomenon in fluid dynamics where a fluid's velocity increases and its pressure decreases as it flows through a constricted section of a pipe or channel. This effect is named after the Italian physicist [[Giovanni Battista Venturi]], who first observed it in the 18th century.
Line 30:
Line 27:
* [[Fluid dynamics]]
* [[Fluid dynamics]]
* [[Flow measurement]]
* [[Flow measurement]]
==References==
* White, F. M. (2011). ''Fluid Mechanics''. McGraw-Hill Education.
[[Category:Fluid dynamics]]
[[Category:Fluid dynamics]]
[[Category:Physics]]
[[Category:Physics]]
== Venturi Effect ==
The '''Venturi effect''' is a phenomenon in fluid dynamics that occurs when a fluid flows through a constricted section of a pipe. This effect is named after the Italian physicist [[Giovanni Battista Venturi]], who first observed it in the 18th century.
== Principles of the Venturi Effect ==
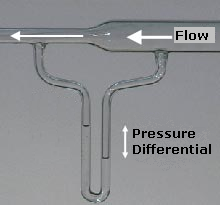
The Venturi effect is based on the principles of [[Bernoulli's principle]], which states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. When a fluid enters a constricted section of a pipe, its velocity must increase to maintain the continuity of flow, as described by the [[continuity equation]].
=== Continuity Equation ===
The [[continuity equation]] is a fundamental principle in fluid dynamics that expresses the conservation of mass. It states that for an incompressible fluid, the mass flow rate must remain constant from one cross-section of a pipe to another. Mathematically, it is expressed as:
: A₁V₁ = A₂V₂
where A is the cross-sectional area and V is the fluid velocity. As the area decreases, the velocity must increase.
=== Bernoulli's Principle ===
[[Bernoulli's principle]] can be expressed as:
: P₁ + ½ρV₁² + ρgh₁ = P₂ + ½ρV₂² + ρgh₂
where P is the pressure, ρ is the fluid density, V is the velocity, g is the acceleration due to gravity, and h is the height above a reference point. In a horizontal pipe, the height terms can be ignored, simplifying the equation to:
: P₁ + ½ρV₁² = P₂ + ½ρV₂²
As the velocity increases in the constricted section, the pressure decreases.
== Applications of the Venturi Effect ==
The Venturi effect has numerous applications in various fields, including:
* [[Venturi meter]]: A device used to measure the flow rate of fluid through a pipe. It consists of a converging section, a throat, and a diverging section.
* [[Carburetor]]: Utilizes the Venturi effect to mix air and fuel in internal combustion engines.
* [[Atomizer]]: Uses the Venturi effect to create a fine spray of liquid.
* [[Aspirator]]: A device that uses the Venturi effect to create a vacuum.
== Medical Applications ==
In the medical field, the Venturi effect is utilized in devices such as:
* [[Venturi mask]]: A medical device used to deliver a known oxygen concentration to patients on controlled oxygen therapy.
* [[Nebulizer]]: Uses the Venturi effect to aerosolize medication for inhalation therapy.
== Conclusion ==
The Venturi effect is a critical concept in fluid dynamics with wide-ranging applications in engineering, medicine, and various industries. Understanding this effect allows for the design and implementation of devices that utilize fluid flow to achieve desired outcomes.
[[Category:Fluid dynamics]]
[[Category:Medical devices]]
{{Fluid dynamics}}
{{Medical devices}}
Latest revision as of 04:38, 29 March 2025
The reduction in fluid pressure that results when a fluid flows through a constricted section of a pipe.
The Venturi effect is a phenomenon in fluid dynamics where a fluid's velocity increases and its pressure decreases as it flows through a constricted section of a pipe or channel. This effect is named after the Italian physicist Giovanni Battista Venturi, who first observed it in the 18th century.
The Venturi effect is a direct consequence of the Bernoulli's principle, which states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. When a fluid enters a constricted section of a pipe, its velocity must increase to maintain the continuity of flow, leading to a drop in pressure.
Illustration of fluid flow through a Venturi tube.
A Venturi tube is a device that utilizes the Venturi effect to measure the flow rate of a fluid. It consists of a tube with a constricted throat that causes a pressure drop, which can be measured to determine the flow rate.
_2006.jpg)
