Compartmental models in epidemiology

Compartmental models in epidemiology are mathematical models used to simplify the mathematical modelling of infectious diseases. These models are a subset of mathematical modelling in epidemiology that use differential equations to describe the dynamics of infection among populations.

Overview

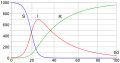
Compartmental models divide the population into different compartments, each representing a specific stage of the epidemic. The most common compartments are Susceptible (S), Infected (I), and Recovered (R), forming the basis of the SIR model. Other models include the SIS model, SEIR model, and MSIR model, each adding additional compartments to represent different stages of disease progression and immunity.

Mathematical Formulation

The mathematical formulation of compartmental models involves a system of differential equations. Each equation represents the rate of change of the population in a compartment. The rates of change are influenced by the parameters of the model, which can include the infection rate, recovery rate, birth rate, and death rate.

Applications

Compartmental models have been used to study a wide range of infectious diseases, including influenza, HIV/AIDS, and COVID-19. They are also used to evaluate the potential impact of public health interventions, such as vaccination and social distancing.

Limitations

While compartmental models are a powerful tool in epidemiology, they have limitations. They assume that the population is homogeneously mixed, which is often not the case in real-world scenarios. They also assume that the parameters of the model are constant, which may not be true in the face of changing social behaviors or evolving pathogens.

See Also

• Mathematical modelling in epidemiology
• Epidemic model
• Basic reproduction number
• Effective reproduction number

References

<references />

This epidemiology-related article is a stub. You can help WikiMD by expanding it.

   This article is a mathematics-related stub. You can help WikiMD by expanding it!

Compartmental models in epidemiology

• 
  SIR model simulated using python
• 
  Graph SIR model without vital dynamics
• 
  Diagram of SIR epidemic model states and transition rates
• 
  SIR trajectory
• 
  SIR model cartoon
• 
  SIR Modell
• 
  SIR model anim
• 
  SIS System Graph
• 
  SIS compartment model
• 
  SIRD
• 
  SIRD model anim
• 
  SIRV model cartoon