Slope: Difference between revisions
CSV import |
CSV import |
||
| Line 30: | Line 30: | ||
{{stub}} | {{stub}} | ||
{{dictionary-stub1}} | {{dictionary-stub1}} | ||
<gallery> | |||
File:Wiki_slope_in_2d.svg|Slope | |||
File:Slope_of_lines_illustrated.jpg|Slope | |||
File:Gradient_of_a_line_in_coordinates_from_-12x+2_to_+12x+2.gif|Slope | |||
File:Slopes_of_Parallel_and_Perpendicular_Lines.svg|Slope | |||
File:Tangent_function_animation.gif|Slope | |||
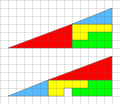
File:Missing_square_puzzle.svg|Slope | |||
File:Nederlands_verkeersbord_J6.svg|Slope | |||
File:PL_road_sign_A-23.svg|Slope | |||
File:Skloník-klesání.jpg|Slope | |||
File:Railway_gradient_post.jpg|Slope | |||
</gallery> | |||
Latest revision as of 12:18, 18 February 2025
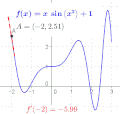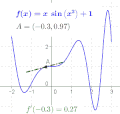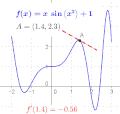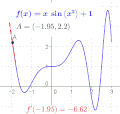
Slope is a fundamental concept in mathematics, specifically in geometry and calculus. It is a measure of the steepness of a line, or a section of a line, connecting two points. In mathematical terms, slope is defined as the ratio of the vertical change (the "rise") to the horizontal change (the "run") between any two points on the line.
Definition[edit]
The slope of a line in the plane containing the x and y axes is generally represented by the letter m, and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. This is commonly referred to as "rise over run". More formally, if the two points are given by the coordinates (x1, y1) and (x2, y2), then the slope m of the line is given by:
m = (y2 - y1) / (x2 - x1)
This formula is known as the slope formula.
Types of Slope[edit]
There are four types of slope: positive, negative, zero, and undefined.
- A positive slope indicates that the y-coordinate increases as the x-coordinate increases. This is represented by a line going up from left to right.
- A negative slope indicates that the y-coordinate decreases as the x-coordinate increases. This is represented by a line going down from left to right.
- A zero slope indicates that the y-coordinate does not change as the x-coordinate changes. This is represented by a horizontal line.
- An undefined slope or infinite slope indicates that the x-coordinate does not change as the y-coordinate changes. This is represented by a vertical line.
Applications[edit]
The concept of slope is used in various branches of mathematics, and it has wide applications in fields like physics, engineering, and economics. For example, in physics, the slope of a position-time graph gives the velocity of the object. In economics, the slope of a demand curve or a supply curve gives the elasticity.
See Also[edit]
|
|
|
-
Slope
-
Slope
-
Slope
-
Slope
-
Slope
-
Slope
-
Slope
-
Slope
-
Slope
-
Slope