Logarithm: Difference between revisions
CSV import |
CSV import |
||
| Line 35: | Line 35: | ||
{{stub}} | {{stub}} | ||
== Logarithm == | |||
<gallery> | |||
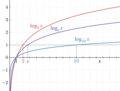
File:Logarithm_plots.png|Logarithm | |||
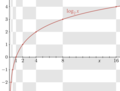
File:Binary_logarithm_plot_with_grid.png|Logarithm | |||
File:Log4.svg|Logarithm | |||
File:Logarithms_Britannica_1797.png|Logarithm | |||
File:Slide_rule_example2_with_labels.svg|Logarithm | |||
File:Logarithm_inversefunctiontoexp.svg|Logarithm | |||
File:Logarithm_derivative.svg|Logarithm | |||
File:Natural_logarithm_integral.svg|Logarithm | |||
File:Natural_logarithm_product_formula_proven_geometrically.svg|Logarithm | |||
File:Logarithm_keys.jpg|Logarithm | |||
File:Taylor_approximation_of_natural_logarithm.gif|Logarithm | |||
File:NautilusCutawayLogarithmicSpiral.jpg|Logarithm | |||
</gallery> | |||
Latest revision as of 11:59, 18 February 2025
Logarithm
The Logarithm is a mathematical concept that is the inverse function to exponentiation. It is used in many areas of science and engineering, including physics, chemistry, biology, and computer science.
History[edit]
The concept of the logarithm was first introduced by John Napier in the early 17th century as a means to simplify calculations. It was later refined and expanded upon by other mathematicians such as Leonhard Euler and Carl Friedrich Gauss.
Definition[edit]
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number x.
Properties[edit]
Logarithms have several important properties that make them useful in many areas of mathematics and science. These include the product rule, the quotient rule, and the power rule.
Applications[edit]
Logarithms are used in many areas of science and engineering. In physics, they are used in the calculation of decibel levels and in the solution of exponential decay problems. In computer science, they are used in the analysis of algorithms and data structures.
See also[edit]
References[edit]
<references />