Multivariable calculus: Difference between revisions
CSV import Tags: mobile edit mobile web edit |
CSV import |
||
| Line 32: | Line 32: | ||
{{Mathematics-stub}} | {{Mathematics-stub}} | ||
<gallery caption="Multivariable_calculus"> | |||
File:((x^2)(y))⁄((x^4)+(y^2)).png|Graph of the function ((x^2)(y))/((x^4)+(y^2)) | |||
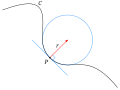
File:Osculating_circle.svg|Osculating circle to a curve | |||
File:Helicoid.svg|Helicoid surface | |||
File:Surface-plot.png|Surface plot of a multivariable function | |||
File:Vector_field.svg|Vector field representation | |||
</gallery> | |||
Latest revision as of 04:31, 18 February 2025
Multivariable Calculus is a branch of mathematics that extends the concepts of calculus to functions of multiple variables. It is also known as multivariate calculus and is a crucial tool in fields such as physics, engineering, and economics where it is used to model and solve problems involving multiple dimensions.
Overview[edit]
Multivariable calculus focuses on the study of functions that have more than one independent variable. Unlike single-variable calculus, which deals with functions of a single variable and their derivatives and integrals, multivariable calculus involves partial derivatives, multiple integrals, and topics such as vector fields and line integrals.
Key Concepts[edit]
Partial Derivatives[edit]
A partial derivative is a derivative in which the change of a function is measured with respect to one of several variables, while the other variables are held constant. It is denoted as \(\frac{\partial f}{\partial x}\) for a function \(f(x, y, ...)\) with respect to variable \(x\).
Multiple Integrals[edit]
Multiple integrals involve integrating a function over a region in two or more dimensions. They are categorized into double integrals, triple integrals, etc., depending on the number of dimensions. These integrals are essential for calculating areas, volumes, and other physical quantities in multiple dimensions.
Vector Calculus[edit]
Vector calculus is a subset of multivariable calculus that deals with vector fields and operations on them. It includes topics such as gradient, divergence, curl, and theorems like Green's, Stokes', and the Divergence Theorem, which relate these operations to integrals over curves, surfaces, and volumes.
Applications[edit]
Multivariable calculus has wide-ranging applications in science and engineering. It is used to model physical phenomena such as electromagnetic fields, fluid dynamics, and heat transfer. In economics, it helps in optimizing functions for cost, revenue, and profit. It also plays a vital role in machine learning and artificial intelligence for optimizing algorithms.
See Also[edit]
References[edit]
<references/>

This article is a mathematics-related stub. You can help WikiMD by expanding it!
- Multivariable_calculus
-
Graph of the function ((x^2)(y))/((x^4)+(y^2))
-
Osculating circle to a curve
-
Helicoid surface
-
Surface plot of a multivariable function
-
Vector field representation