Continuous-time Markov chain

Continuous-time Markov chain (CTMC) is a stochastic process that describes a sequence of events occurring in continuous time where the probability of each event depends only on the state attained in the previous event. This mathematical model is a generalization of the Markov chain to the continuous-time domain. CTMCs are widely used in various fields such as queueing theory, telecommunications, bioinformatics, and finance to model systems that transition from one state to another over continuous time intervals.

Definition

A Continuous-time Markov chain is defined by a countable state space S, a transition rate matrix Q with elements q_ij, and an initial state distribution. The element q_ij of the matrix Q represents the rate at which transitions from state i to state j occur. For a CTMC, the time spent in each state before making a transition to another state is exponentially distributed.

Properties

CTMCs possess the Markov property, which states that the future state of the process depends only on the current state and not on the sequence of events that preceded it. This memoryless property simplifies the analysis and modeling of complex systems.

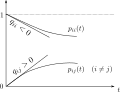
Transition Probabilities

The transition probabilities of a CTMC, denoted by P(t) = [p_ij(t)], where p_ij(t) is the probability of transitioning from state i to state j in time t, can be determined using the Kolmogorov forward and backward equations. These differential equations describe how the transition probabilities change over time.

Applications

Continuous-time Markov chains are used in a variety of applications:

• In queueing theory, CTMCs model systems like customer service centers where events (e.g., arrivals and departures) occur continuously over time.
• In telecommunications, they are used to model packet traffic and channel access protocols.
• In bioinformatics, CTMCs are applied in the modeling of gene sequence evolution.
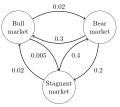
• In finance, they are used to model the transitions in credit ratings of companies or the changes in interest rates.

Examples

One of the simplest examples of a CTMC is the Poisson process, which models the occurrence of events that happen independently at a constant average rate.

Challenges and Solutions

Analyzing and computing the properties of CTMCs can be challenging, especially for large state spaces. Numerical methods and approximation techniques, such as uniformization, are often employed to overcome these challenges.

See Also

• Markov chain
• Stochastic process
• Poisson process
• Queueing theory

References

<references/>

   This article is a mathematics-related stub. You can help WikiMD by expanding it!

• 
  Intensities vs Transition Probabilities
• 
  Financial Markov Process
• 
  Transition Graph Pac-Man