Armstrong limit: Difference between revisions

Revision as of 18:48, 11 February 2025

Minimum distance from the center to the side of a regular polygon

The apothem of a regular polygon is the distance from the center to the midpoint of one of its sides. It is a key concept in geometry, particularly in the study of regular polygons, and is used in various calculations, including the area of the polygon.

Definition

In a regular polygon, all sides and angles are equal. The apothem is the perpendicular distance from the center of the polygon to one of its sides. It can also be considered as the radius of the inscribed circle (incircle) of the polygon.

Properties

The apothem is an important element in determining the area of a regular polygon. The formula for the area \(A\) of a regular polygon with \(n\) sides, each of length \(s\), and apothem \(a\) is given by:

\[ A = \frac{1}{2} \times n \times s \times a \]

This formula can also be expressed in terms of the perimeter \(P\) of the polygon:

\[ A = \frac{1}{2} \times P \times a \]

Calculation

The apothem can be calculated if the side length \(s\) and the number of sides \(n\) of the regular polygon are known. The formula for the apothem \(a\) is:

\[ a = \frac{s}{2 \tan(\pi/n)} \]

This formula arises from the fact that the apothem is the adjacent side of a right triangle formed by the radius of the circumscribed circle, the apothem itself, and half of a side of the polygon.

Applications

The apothem is used in various applications, including:

Calculating the area of regular polygons.
Determining the radius of the inscribed circle.
Architectural design and construction, where regular polygons are used in tiling and other patterns.

Examples

For a regular hexagon with side length \(s\), the apothem can be calculated using the formula:

\[ a = \frac{s}{2 \tan(\pi/6)} = \frac{s}{\sqrt{3}} \]

This is because a regular hexagon can be divided into six equilateral triangles, and the apothem is the height of one of these triangles.

Related pages

Gallery

Diagram showing the apothem of a hexagon

@@ Line 1: / Line 1: @@
-'''Armstrong Limit''' is a measure of altitude above which atmospheric pressure is sufficiently low that water boils at the normal temperature of the human body. It is named after [[Harry George Armstrong]], an American physician, who founded the field of [[aerospace medicine]].
+{{Short description|Minimum distance from the center to the side of a regular polygon}}
-== Overview ==
+The '''apothem''' of a regular polygon is the distance from the center to the midpoint of one of its sides. It is a key concept in geometry, particularly in the study of regular polygons, and is used in various calculations, including the area of the polygon.
-The Armstrong Limit is defined as the altitude at which the atmospheric pressure is down to 6.3 kPa (47 mm Hg), which is a level at which water boils at 37°C (98.6°F), the normal body temperature of humans. This limit is located at an altitude of about 18–19 km (11–12 miles) above sea level under average atmospheric conditions.
-== Implications ==
+==Definition==
-Above the Armstrong Limit, exposed body fluids such as saliva, tears, urine, and the water in lungs and tissues would boil away without a full-body pressure suit or a pressurized capsule. However, the skin and circulatory system can prevent this effect and keep the body under pressure, but this is not enough to keep the body safe for more than a few minutes.
+In a regular polygon, all sides and angles are equal. The apothem is the perpendicular distance from the center of the polygon to one of its sides. It can also be considered as the radius of the inscribed circle (incircle) of the polygon.
-== Safety Measures ==
+==Properties==
-To survive above the Armstrong Limit, humans must wear a full pressure suit or be within a pressurized capsule. This is why astronauts wear pressure suits during certain phases of spaceflight, and why high-altitude pilots and balloonists use pressure suits or pressurized capsules.
+The apothem is an important element in determining the area of a regular polygon. The formula for the area \(A\) of a regular polygon with \(n\) sides, each of length \(s\), and apothem \(a\) is given by:
-== See Also ==
+\[
-* [[Aerospace Medicine]]
+A = \frac{1}{2} \times n \times s \times a
-* [[Atmospheric Pressure]]
+\]
-* [[Pressure Suit]]
-* [[Space Medicine]]
-== References ==
+This formula can also be expressed in terms of the perimeter \(P\) of the polygon:
-<references />
-{{stub}}
+\[
+A = \frac{1}{2} \times P \times a
+\]
-[[Category:Medicine]]
+==Calculation==
-[[Category:Aerospace Medicine]]
+The apothem can be calculated if the side length \(s\) and the number of sides \(n\) of the regular polygon are known. The formula for the apothem \(a\) is:
-[[Category:Atmospheric Science]]
+\[
+a = \frac{s}{2 \tan(\pi/n)}
+\]
+This formula arises from the fact that the apothem is the adjacent side of a right triangle formed by the radius of the circumscribed circle, the apothem itself, and half of a side of the polygon.
+==Applications==
+The apothem is used in various applications, including:
+* Calculating the area of regular polygons.
+* Determining the radius of the inscribed circle.
+* Architectural design and construction, where regular polygons are used in tiling and other patterns.
+==Examples==
+For a regular hexagon with side length \(s\), the apothem can be calculated using the formula:
+\[
+a = \frac{s}{2 \tan(\pi/6)} = \frac{s}{\sqrt{3}}
+\]
+This is because a regular hexagon can be divided into six equilateral triangles, and the apothem is the height of one of these triangles.
+==Related pages==
+* [[Regular polygon]]
+* [[Circumscribed circle]]
+* [[Inscribed circle]]
+* [[Perimeter]]
+==Gallery==
+<gallery>
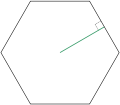
+File:Apothem_of_hexagon.svg|Diagram showing the apothem of a hexagon
+</gallery>
+[[Category:Geometry]]