Trigonometric functions: Difference between revisions

From WikiMD's Wellness Encyclopedia

Newer edit →
CSV import
 
CSV import
Line 1: Line 1:
{{png-image}}
== Trigonometric Functions ==
The '''trigonometric functions''' are [[mathematics|mathematical]] functions that relate the angles of a [[triangle]] to the lengths of its sides. They are fundamental in the study of [[geometry]], [[physics]], [[engineering]], and many other fields. The most commonly used trigonometric functions are sine, cosine, and tangent, often abbreviated as sin, cos, and tan, respectively. These functions are defined for [[angle]]s, which can be measured in [[radian]]s or degrees.


==Definition==
Trigonometric functions are fundamental mathematical functions that relate the angles of a triangle to the lengths of its sides. They are widely used in various fields such as [[mathematics]], [[physics]], [[engineering]], and [[computer science]]. The primary trigonometric functions are the sine, cosine, and tangent, which are defined for angles in a right triangle or on the unit circle.
Trigonometric functions are defined using a [[right-angled triangle]] or a [[unit circle]] (a circle with a radius of one unit). For angles in a right-angled triangle, the sine of an angle is the ratio of the length of the opposite side to the length of the [[hypotenuse]], the cosine is the ratio of the length of the adjacent side to the hypotenuse, and the tangent is the ratio of the length of the opposite side to the length of the adjacent side.


In the context of the unit circle, these functions are defined for any real angle as follows:
=== Definitions ===
* The sine of an angle is the y-coordinate of the point on the unit circle at that angle,
* The cosine of an angle is the x-coordinate,
* The tangent of an angle is the y-coordinate divided by the x-coordinate (when the x-coordinate is not zero).


==Properties and Applications==
The six main trigonometric functions are:
Trigonometric functions have many important properties, such as periodicity and symmetry. They are periodic in that they repeat their values in regular intervals, making them especially useful in the analysis of [[wave]]s and oscillations. The sine and cosine functions, for example, have a period of \(2\pi\) radians (or 360 degrees), meaning that their values repeat every \(2\pi\) radians.


These functions are also used to solve [[triangle]]s, particularly in [[trigonometry]], where the lengths of a triangle's sides and its angles are related. This is crucial in many areas of [[applied mathematics]], [[physics]], and [[engineering]], such as in the design of structures, the analysis of waves, and in navigation.
* '''Sine (sin)''': In a right triangle, the sine of an angle is the ratio of the length of the opposite side to the hypotenuse.
* '''Cosine (cos)''': The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse.
* '''Tangent (tan)''': The tangent of an angle is the ratio of the sine to the cosine, or equivalently, the opposite side to the adjacent side.
* '''Cosecant (csc)''': The cosecant is the reciprocal of the sine.
* '''Secant (sec)''': The secant is the reciprocal of the cosine.
* '''Cotangent (cot)''': The cotangent is the reciprocal of the tangent.


==Extensions==
=== Unit Circle ===
Beyond the basic trigonometric functions, there are several related functions that are useful in various contexts. These include:
* The [[secant]] (sec), which is the reciprocal of the cosine,
* The [[cosecant]] (csc), the reciprocal of the sine,
* The [[cotangent]] (cot), the reciprocal of the tangent.


There are also [[hyperbolic trigonometric functions]] which are analogs of the trigonometric functions but for a hyperbola instead of a circle. These include hyperbolic sine (sinh), hyperbolic cosine (cosh), and hyperbolic tangent (tanh), among others.
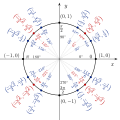
The unit circle is a circle with a radius of one centered at the origin of the coordinate plane. It is a fundamental tool in trigonometry, allowing the extension of trigonometric functions to all real numbers. The angle in the unit circle is measured from the positive x-axis, and the coordinates of a point on the unit circle are \((\cos \theta, \sin \theta)\).


==Complex Numbers==
[[File:Unit_Circle_Definitions_of_Six_Trigonometric_Functions.svg|thumb|right|Unit circle definitions of trigonometric functions]]
Trigonometric functions can also be defined for [[complex number]]s, greatly extending their applicability. This is done using [[Euler's formula]], which relates complex exponentials to trigonometric functions, providing a powerful tool in [[complex analysis]] and other areas of mathematics.
 
=== Periodicity and Symmetry ===
 
Trigonometric functions are periodic, meaning they repeat their values in regular intervals. The sine and cosine functions have a period of \(2\pi\), while the tangent and cotangent have a period of \(\pi\). These functions also exhibit symmetry properties:
 
* '''Even functions''': Cosine and secant are even functions, meaning \(\cos(-\theta) = \cos(\theta)\).
* '''Odd functions''': Sine, tangent, cosecant, and cotangent are odd functions, meaning \(\sin(-\theta) = -\sin(\theta)\).
 
=== Graphs ===
 
The graphs of trigonometric functions are wave-like and exhibit periodic behavior. The sine and cosine functions produce smooth, continuous waves, while the tangent function has vertical asymptotes and repeats every \(\pi\) radians.
 
[[File:Periodic_sine.svg|thumb|right|Graph of the sine function]]
 
=== Applications ===
 
Trigonometric functions are used in various applications, including:
 
* '''Wave analysis''': Modeling sound waves, light waves, and other periodic phenomena.
* '''Engineering''': Calculating forces, angles, and distances in mechanical and civil engineering.
* '''Astronomy''': Determining the positions of celestial bodies.
* '''Computer graphics''': Rotating and transforming objects in 3D space.
 
=== Related Functions ===
 
Trigonometric functions are closely related to the exponential function through Euler's formula, which connects complex exponentials to trigonometric functions:
 
\[ e^{i\theta} = \cos \theta + i\sin \theta \]
 
=== Related Pages ===


==See Also==
* [[Inverse trigonometric functions]]
* [[Trigonometry]]
* [[Trigonometry]]
* [[Unit circle]]
* [[Unit circle]]
* [[Fourier series]]
* [[Euler's formula]]
* [[Euler's formula]]


[[Category:Mathematics]]
== Gallery ==
 
<gallery>
File:Academ_Base_of_trigonometry.svg|Base of trigonometry
File:TrigonometryTriangle.svg|Trigonometry triangle
File:TrigFunctionDiagram.svg|Diagram of trigonometric functions
File:Circle-trig6.svg|Circle with trigonometric functions
File:Unit_Circle_Definitions_of_Six_Trigonometric_Functions.svg|Unit circle definitions
File:trigonometric_function_quadrant_sign.svg|Quadrant signs of trigonometric functions
File:Trigonometric_functions.svg|Trigonometric functions
File:Unit_circle_angles_color.svg|Unit circle angles
File:Taylorsine.svg|Taylor series of sine
File:Taylor_cos.gif|Taylor series of cosine
File:Taylorreihenentwicklung_des_Kosinus.svg|Taylor series expansion of cosine
File:Sinus_und_Kosinus_am_Einheitskreis_3.svg|Sine and cosine on the unit circle
File:Trig-sin.png|Graph of sine
File:Trig-cos.png|Graph of cosine
File:Trig-tan.png|Graph of tangent
File:Trig-cot.png|Graph of cotangent
File:Trig-sec.png|Graph of secant
File:Trig-csc.png|Graph of cosecant
File:Lissajous_curve_5by4.svg|Lissajous curve
File:Synthesis_square.gif|Square wave synthesis
File:Sawtooth_Fourier_Animation.gif|Sawtooth Fourier animation
</gallery>
 
{{Trigonometry}}
[[Category:Trigonometry]]
[[Category:Trigonometry]]
{{math-stub}}

Revision as of 01:08, 10 February 2025

Trigonometric Functions

Trigonometric functions are fundamental mathematical functions that relate the angles of a triangle to the lengths of its sides. They are widely used in various fields such as mathematics, physics, engineering, and computer science. The primary trigonometric functions are the sine, cosine, and tangent, which are defined for angles in a right triangle or on the unit circle.

Definitions

The six main trigonometric functions are:

  • Sine (sin): In a right triangle, the sine of an angle is the ratio of the length of the opposite side to the hypotenuse.
  • Cosine (cos): The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse.
  • Tangent (tan): The tangent of an angle is the ratio of the sine to the cosine, or equivalently, the opposite side to the adjacent side.
  • Cosecant (csc): The cosecant is the reciprocal of the sine.
  • Secant (sec): The secant is the reciprocal of the cosine.
  • Cotangent (cot): The cotangent is the reciprocal of the tangent.

Unit Circle

The unit circle is a circle with a radius of one centered at the origin of the coordinate plane. It is a fundamental tool in trigonometry, allowing the extension of trigonometric functions to all real numbers. The angle in the unit circle is measured from the positive x-axis, and the coordinates of a point on the unit circle are \((\cos \theta, \sin \theta)\).

File:Unit Circle Definitions of Six Trigonometric Functions.svg
Unit circle definitions of trigonometric functions

Periodicity and Symmetry

Trigonometric functions are periodic, meaning they repeat their values in regular intervals. The sine and cosine functions have a period of \(2\pi\), while the tangent and cotangent have a period of \(\pi\). These functions also exhibit symmetry properties:

  • Even functions: Cosine and secant are even functions, meaning \(\cos(-\theta) = \cos(\theta)\).
  • Odd functions: Sine, tangent, cosecant, and cotangent are odd functions, meaning \(\sin(-\theta) = -\sin(\theta)\).

Graphs

The graphs of trigonometric functions are wave-like and exhibit periodic behavior. The sine and cosine functions produce smooth, continuous waves, while the tangent function has vertical asymptotes and repeats every \(\pi\) radians.

File:Periodic sine.svg
Graph of the sine function

Applications

Trigonometric functions are used in various applications, including:

  • Wave analysis: Modeling sound waves, light waves, and other periodic phenomena.
  • Engineering: Calculating forces, angles, and distances in mechanical and civil engineering.
  • Astronomy: Determining the positions of celestial bodies.
  • Computer graphics: Rotating and transforming objects in 3D space.

Related Functions

Trigonometric functions are closely related to the exponential function through Euler's formula, which connects complex exponentials to trigonometric functions:

\[ e^{i\theta} = \cos \theta + i\sin \theta \]

Related Pages

Gallery

Template:Trigonometry

Retrieved from "https://wikimd.com/index.php?title=Trigonometric_functions&oldid=6201665"