Dodecahedron: Difference between revisions
CSV import |
CSV import |
||
| Line 26: | Line 26: | ||
[[Category:Geometry]] | [[Category:Geometry]] | ||
[[Category:Polyhedra]] | [[Category:Polyhedra]] | ||
<gallery> | |||
File:Dodecahedron.png|Dodecahedron | |||
File:Small_stellated_dodecahedron.png|Small Stellated Dodecahedron | |||
File:Great_dodecahedron.png|Great Dodecahedron | |||
File:Great_stellated_dodecahedron.png|Great Stellated Dodecahedron | |||
File:Pyritohedron.png|Pyritohedron | |||
File:Tetartoid.png|Tetartoid | |||
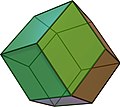
File:Rhombicdodecahedron.jpg|Rhombic Dodecahedron | |||
File:Snub_disphenoid.png|Snub Disphenoid | |||
File:Rhombo-hexagonal_dodecahedron.png|Rhombo-hexagonal Dodecahedron | |||
File:Squared_rhombic_dodecahedron.png|Squared Rhombic Dodecahedron | |||
File:Trapezo-rhombic_dodecahedron.png|Trapezo-rhombic Dodecahedron | |||
File:Triangular_square_dodecahedron.png|Triangular Square Dodecahedron | |||
</gallery> | |||
<gallery> | <gallery> | ||
File:Dodecahedron.png|Dodecahedron | File:Dodecahedron.png|Dodecahedron | ||
Latest revision as of 12:25, 18 February 2025

Dodecahedron refers to any polyhedron with twelve flat faces. The most recognized form of a dodecahedron is the regular dodecahedron, which is one of the five Platonic solids. A regular dodecahedron features twelve regular pentagonal faces, with three meeting at each vertex. It has 20 vertices and 30 edges.
Properties[edit]
The regular dodecahedron has a rich set of properties that have fascinated mathematicians, artists, and philosophers since antiquity. Its symmetry is described by the icosahedral symmetry group, which is one of the most symmetrical groups in three dimensions. The dual polyhedron of a regular dodecahedron is the icosahedron, another Platonic solid, which has twenty triangular faces, twelve vertices, and thirty edges.
Mathematical Dimensions[edit]
For a regular dodecahedron with side length a, the surface area A and the volume V can be calculated using the following formulas:
- Surface area: \(A = 3\sqrt{25 + 10\sqrt{5}}a^2\)
- Volume: \(V = \frac{15 + 7\sqrt{5}}{4}a^3\)
These formulas highlight the relationship between the geometry of the dodecahedron and the golden ratio, as \(\phi = \frac{1 + \sqrt{5}}{2}\) appears in the derivation of these expressions.
Applications and Cultural Significance[edit]
The dodecahedron has been used in various contexts throughout history. In Platonism, the dodecahedron is often associated with the universe, representing the ether or the heavens due to its perfect symmetry. In modern times, dodecahedra appear in various fields such as crystallography, where certain crystals naturally form dodecahedral shapes, and in board games and role-playing games, where twelve-sided dice are commonly used.
Variants[edit]
Besides the regular dodecahedron, there are many other types of dodecahedra, categorized by their properties and construction methods. The rhombic dodecahedron is another notable variant, which is a convex polyhedron with twelve rhombic faces. It serves as the dual polyhedron to the cuboctahedron and has applications in crystallography and in dividing space into equal volume cells with minimal surface area.
See Also[edit]
-
Dodecahedron
-
Small Stellated Dodecahedron
-
Great Dodecahedron
-
Great Stellated Dodecahedron
-
Pyritohedron
-
Tetartoid
-
Rhombic Dodecahedron
-
Snub Disphenoid
-
Rhombo-hexagonal Dodecahedron
-
Squared Rhombic Dodecahedron
-
Trapezo-rhombic Dodecahedron
-
Triangular Square Dodecahedron
-
Dodecahedron
-
Small Stellated Dodecahedron
-
Great Dodecahedron
-
Great Stellated Dodecahedron
-
Pyritohedron
-
Tetartoid
-
Rhombic Dodecahedron
-
Snub Disphenoid
-
Rhombo-hexagonal Dodecahedron
-
Squared Rhombic Dodecahedron
-
Trapezo-rhombic Dodecahedron
-
Triangular Square Dodecahedron