Adjacency matrix: Difference between revisions
CSV import |
CSV import |
||
| Line 53: | Line 53: | ||
[[Category:Graph theory]] | [[Category:Graph theory]] | ||
<gallery> | |||
File:6n-graph2.svg|Adjacency matrix of a 6-node graph | |||
File:Symmetric_group_4;_Cayley_graph_1,5,21_(Nauru_Petersen);_numbers.svg|Cayley graph of the symmetric group S4 with generators 1, 5, 21 (Nauru Petersen) | |||
File:Symmetric_group_4;_Cayley_graph_1,5,21_(adjacency_matrix).svg|Adjacency matrix of the Cayley graph of S4 with generators 1, 5, 21 | |||
File:Symmetric_group_4;_Cayley_graph_4,9;_numbers.svg|Cayley graph of the symmetric group S4 with generators 4, 9 | |||
File:Symmetric_group_4;_Cayley_graph_4,9_(adjacency_matrix).svg|Adjacency matrix of the Cayley graph of S4 with generators 4, 9 | |||
</gallery> | |||
Latest revision as of 10:54, 18 February 2025
Adjacency Matrix[edit]
An adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the context of an undirected graph, the adjacency matrix is symmetric.
Definition[edit]
For a simple graph with n vertices, the adjacency matrix is an n _ n matrix A where the non-diagonal entry aij is the number of edges from vertex i to vertex j, and the diagonal entry aii is the number of loops at vertex i.
In the case of an undirected graph, the adjacency matrix is symmetric. If the graph is weighted, the elements of the matrix are the weights of the edges.
Properties[edit]
- The adjacency matrix of a simple graph is a binary matrix.
- The degree of a vertex in a graph can be determined by summing the entries in the corresponding row (or column) of the adjacency matrix.
- The adjacency matrix of a complete graph has all off-diagonal entries equal to 1.
- The adjacency matrix of a bipartite graph can be permuted to have a block form with zero diagonal blocks.
Applications[edit]
Adjacency matrices are used in various applications, including:
Examples[edit]
Symmetric Group 4[edit]
The symmetric group on 4 elements, denoted as S4, can be represented by various Cayley graphs. Below are examples of adjacency matrices for different Cayley graphs of S4:
- Cayley graph with generators {1, 5, 21}:
*

- Cayley graph with generators {4, 9}:
*

Related Pages[edit]
Gallery[edit]
-
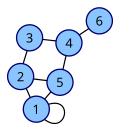
Example of a graph represented by an adjacency matrix
-
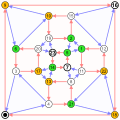
Cayley graph with generators {1, 5, 21}
-
Cayley graph with generators {4, 9}
-
Adjacency matrix of a 6-node graph
-
Cayley graph of the symmetric group S4 with generators 1, 5, 21 (Nauru Petersen)
-
Adjacency matrix of the Cayley graph of S4 with generators 1, 5, 21
-
Cayley graph of the symmetric group S4 with generators 4, 9
-
Adjacency matrix of the Cayley graph of S4 with generators 4, 9