Trajectory: Difference between revisions
CSV import |
CSV import |
||
| Line 46: | Line 46: | ||
[[Category:Physics]] | [[Category:Physics]] | ||
[[Category:Mechanics]] | [[Category:Mechanics]] | ||
<gallery> | |||
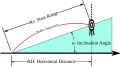
File:RiflemansRule.svg|Rifleman's Rule | |||
File:Inclinedthrow.gif|Inclined Throw | |||
File:Ideal_projectile_motion_for_different_angles.svg|Ideal Projectile Motion for Different Angles | |||
File:Selomie_Melkie_-_Forensics_Final_Project_(5).jpg|Trajectory | |||
</gallery> | |||
Latest revision as of 04:31, 18 February 2025
Trajectory[edit]
A trajectory is the path that a moving object follows through space as a function of time. It is often associated with the motion of projectiles, such as bullets, balls, or any object that is thrown, shot, or propelled. The study of trajectories is a fundamental aspect of physics and engineering, particularly in the fields of ballistics and aerodynamics.
Physics of Trajectories[edit]
The trajectory of an object is determined by the initial velocity, the angle of launch, and the forces acting on the object, such as gravity and air resistance. In a vacuum, the only force acting on a projectile is gravity, which causes the object to follow a parabolic path. This is known as projectile motion.

In the presence of air resistance, the trajectory is more complex and is no longer a perfect parabola. The object will experience a deceleration due to the drag force, which depends on the shape, size, and speed of the object, as well as the density of the air.
Calculating Trajectories[edit]
The calculation of a trajectory involves solving the equations of motion, which are derived from Newton's laws of motion. For a simple projectile in a vacuum, the horizontal and vertical components of motion can be analyzed separately. The horizontal motion is uniform, while the vertical motion is uniformly accelerated due to gravity.

For more complex scenarios, such as when air resistance is significant, numerical methods or computer simulations are often used to predict the trajectory.
Applications[edit]
Understanding trajectories is crucial in many fields. In sports, athletes use knowledge of trajectories to improve their performance in activities such as basketball, golf, and archery. In military applications, accurate prediction of projectile trajectories is essential for targeting and ballistics.

In space exploration, calculating the trajectories of spacecraft is vital for mission planning and execution. Engineers must account for gravitational forces from celestial bodies and other factors to ensure that spacecraft reach their intended destinations.
Related Pages[edit]
References[edit]
- Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics. Wiley.
- Tipler, P. A., & Mosca, G. (2008). Physics for Scientists and Engineers. W. H. Freeman.

-
Rifleman's Rule
-
Inclined Throw
-
Ideal Projectile Motion for Different Angles
-
Trajectory