Material nonimplication: Difference between revisions
CSV import |
CSV import |
||
| Line 52: | Line 52: | ||
{{logic-stub}} | {{logic-stub}} | ||
<gallery caption="Material_nonimplication"> | |||
File:Venn0100.svg|Material_nonimplication | |||
File:Venn0100.svg|Material_nonimplication | |||
File:Venn1011.svg|Material_nonimplication | |||
File:Venn0100.svg|Material_nonimplication | |||
File:Venn1010.svg|Material_nonimplication | |||
File:Venn0011.svg|Material_nonimplication | |||
File:Venn0101.svg|Material_nonimplication | |||
File:Venn1100.svg|Material_nonimplication | |||
</gallery> | |||
Latest revision as of 11:16, 18 February 2025
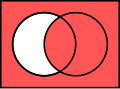
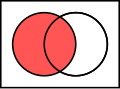
Material nonimplication is a logical operation that is symbolized by the arrow \(\rightarrow\) in reverse, often represented as \(\nrightarrow\). It is a binary operation on two logical values, typically the values of two propositions, that produces a value of false only in the case where the first operand is true and the second operand is false. In all other cases, it produces a true value. This operation is the logical equivalent of saying "if not P, then Q" and is also known as the abjunction operation.
Definition[edit]
Given two propositions, \(P\) and \(Q\), the material nonimplication of \(P\) and \(Q\) (denoted as \(P \nrightarrow Q\)) can be defined truthfully in a truth table:
| \(P\) | \(Q\) | \(P \nrightarrow Q\) |
|---|---|---|
| True | True | False |
| True | False | True |
| False | True | False |
| False | False | False |
The only case where \(P \nrightarrow Q\) is true is when \(P\) is true and \(Q\) is false. In all other cases, the result is false.
Relation to Other Logical Operations[edit]
Material nonimplication is closely related to other logical operations such as Material implication (\(P \rightarrow Q\)), Negation (\(\neg\)), and Conjunction (\(P \land Q\)). It can be expressed using these operations in several ways, for example, \(P \nrightarrow Q\) is equivalent to \(P \land \neg Q\).
Material Implication[edit]
Material implication and material nonimplication are inversely related. While material implication asserts a false value only when the first operand is true and the second is false, material nonimplication asserts a true value in this case.
Negation and Conjunction[edit]
Material nonimplication can be seen as the conjunction of the first proposition with the negation of the second proposition, symbolically represented as \(P \land \neg Q\).
Applications[edit]
Material nonimplication has applications in various fields of logic, computer science, and mathematics, particularly in the construction of logical proofs, the design of digital circuits, and the formulation of mathematical conjectures.
See Also[edit]
- Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication
-
Material_nonimplication