Poisson distribution: Difference between revisions
CSV import |
CSV import Tags: mobile edit mobile web edit |
||
| Line 38: | Line 38: | ||
{{stub}} | {{stub}} | ||
{{dictionary-stub1}} | {{dictionary-stub1}} | ||
<gallery> | |||
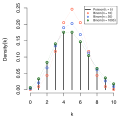
File:Poisson_pmf.svg|Probability mass function of a Poisson distribution | |||
File:Poisson_cdf.svg|Cumulative distribution function of a Poisson distribution | |||
File:Chewing_gum_on_a_sidewalk_in_Reykjavík.JPG|Chewing gum on a sidewalk in Reykjavík | |||
File:Binomial_versus_poisson.svg|Comparison of binomial and Poisson distributions | |||
</gallery> | |||
Latest revision as of 04:35, 18 February 2025
Poisson Distribution is a probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. The distribution was named after French mathematician Siméon Denis Poisson.
Definition[edit]
The Poisson distribution can be defined in terms of the probability mass function (PMF). The PMF of a Poisson distribution is given by:
where:
- is the average rate of value (the parameter of the distribution, also called the rate or rate parameter),
- is the number of occurrences of an event — the event can be anything that is countable (number of phone calls received by a call center per hour or the number of decay events per second from a radioactive source),
- is the base of the natural logarithm (approximately equal to 2.71828),
- is the factorial of k.
Properties[edit]
The Poisson distribution has several unique properties, including:
- The mean and variance of a Poisson distribution are both equal to .
- The mode of a Poisson distribution is approximately for .
- The skewness of a Poisson distribution is .
- The kurtosis of a Poisson distribution is .
Applications[edit]
The Poisson distribution is used in many areas of science and engineering, including physics, biology, telecommunications, insurance, queueing theory, and reliability engineering. It is particularly useful in situations where events occur randomly and independently, and the average rate of occurrence is known.
See also[edit]
References[edit]
<references />