Brownian motion

Brownian motion is a phenomenon observed in the field of physics and mathematics, named after the botanist Robert Brown. It refers to the random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collision with the fast-moving molecules in the fluid.

History

The phenomenon of Brownian motion was first observed by the botanist Robert Brown in 1827. Brown was studying pollen particles floating in water under a microscope when he noticed that the particles moved in a random, jittery manner. This movement was later named "Brownian motion" in his honor.

Explanation

Brownian motion can be explained by the kinetic theory of gases. According to this theory, the molecules of a gas are in constant, random motion, and their impact on small visible particles causes the latter to move in a similar random fashion. This is the underlying principle of Brownian motion.

Mathematical Description

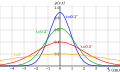
The mathematical description of Brownian motion involves stochastic processes and differential equations. The motion of a particle undergoing Brownian motion can be modeled by a Wiener process, a continuous-time stochastic process that is widely used in finance and other fields.

Applications

Brownian motion has applications in various fields such as physics, chemistry, engineering, and finance. In physics and chemistry, it is used to explain the diffusion process. In finance, it is used in the Black-Scholes model for option pricing.

See Also

• Random walk
• Diffusion
• Stochastic process
• Wiener process

   This article is a physics-related stub. You can help WikiMD by expanding it!

   This article is a mathematics-related stub. You can help WikiMD by expanding it!

• 
  2D Random Walk of Ag Adatom on Ag(111)
• 
  Brownian Motion Large
• 
  Perrin's Plot of Brownian Motion
• 
  Diffusion of Brownian Particles
• 
  Brownian Motion Gamboge
• 
  Brownian Motion
• 
  2D Random Walk 400x400
• 
  Wiener Process 3D
• 
  Brownian Motion on Sphere