Gauss's law: Difference between revisions
CSV import Tags: mobile edit mobile web edit |
CSV import |
||
| Line 37: | Line 37: | ||
[[Category:Maxwell's equations]] | [[Category:Maxwell's equations]] | ||
[[Category:Scientific laws named after people]] | [[Category:Scientific laws named after people]] | ||
== Gauss's law == | |||
<gallery> | |||
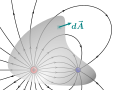
File:Maxwell_integral_Gauss_sphere.svg|Illustration of Gauss's law with a sphere | |||
File:Electric-flux-surface-example.svg|Example of electric flux through a surface | |||
File:Electric-flux-no-charge-inside.svg|Electric flux with no charge inside | |||
File:Gauss's_law_-_surface_charge_-_boundary_condition_on_D.svg|Gauss's law with surface charge and boundary condition on D | |||
</gallery> | |||
Latest revision as of 05:05, 18 February 2025
Gauss's Law is a fundamental law in electrostatics that describes the relationship between electric fields and the charges that cause them. Named after the German mathematician and physicist Carl Friedrich Gauss, this law is one of the four Maxwell's equations that form the foundation of classical electrodynamics, classical optics, and electric circuits.
Etymology[edit]
The law is named after Carl Friedrich Gauss, a German mathematician and physicist who made significant contributions to many fields, including number theory, algebra, statistics, analysis, differential geometry, geodesy, geophysics, mechanics, electrostatics, magnetic fields, astronomy, matrix theory, and optics.
Definition[edit]
Gauss's Law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the electric constant. Mathematically, it is expressed as:
∮ E • dA = Q / ε0
where:
- ∮ E • dA is the electric flux through a closed surface,
- Q is the total charge enclosed by the surface, and
- ε0 is the electric constant.
Applications[edit]
Gauss's Law is used in various fields of physics, including electrostatics and magnetostatics. It is also used to derive Coulomb's Law, and to calculate the electric field in various situations.
Related Terms[edit]
See Also[edit]
References[edit]
<references />