Factor analysis: Difference between revisions
CSV import Tags: mobile edit mobile web edit |
CSV import |
||
| Line 1: | Line 1: | ||
{{short description|Statistical method used to describe variability among observed variables}} | |||
==Overview== | == Overview == | ||
Factor analysis | [[File:FactorPlot.svg|thumb|right|A graphical representation of factor analysis results.]] | ||
'''Factor analysis''' is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. The observed variables are modeled as linear combinations of the potential factors, plus "error" terms. The information gained about the interdependencies can be used later to reduce the set of variables in a dataset. | |||
== | == History == | ||
The | Factor analysis originated in psychometrics and is used in behavioral sciences, social sciences, marketing, product management, operations research, and other applied sciences that deal with large quantities of data. The method was first introduced by [[Charles Spearman]] in the early 20th century. | ||
== Types of Factor Analysis == | |||
There are two main types of factor analysis: | |||
* '''Exploratory Factor Analysis (EFA)''': Used to identify the underlying relationship between measured variables. It is often used when the researcher does not have a preconceived idea of the structure or number of factors. | |||
* '''Confirmatory Factor Analysis (CFA)''': Used to test the hypothesis that the relationships between observed variables and their underlying latent constructs exist. It is often used when the researcher has a specific idea about the structure or number of factors. | |||
Factor | |||
== Applications == | |||
Factor analysis is widely used in various fields: | |||
* In [[psychology]], it is used to identify latent constructs such as intelligence, personality traits, and other psychological phenomena. | |||
* In [[marketing]], it helps in identifying underlying factors that affect consumer behavior and preferences. | |||
* In [[finance]], it is used to identify factors that affect stock prices and market trends. | |||
== | == Methodology == | ||
The process of factor analysis involves several steps: | |||
1. '''Data Collection''': Gather data on the variables of interest. | |||
2. '''Correlation Matrix''': Compute the correlation matrix of the variables. | |||
3. '''Extraction of Factors''': Use methods such as principal component analysis or maximum likelihood to extract factors. | |||
4. '''Rotation''': Apply rotation methods like varimax or promax to achieve a simpler and more interpretable factor structure. | |||
5. '''Interpretation''': Analyze the factor loadings to interpret the factors. | |||
== Limitations == | |||
Factor analysis has several limitations: | |||
* It requires a large sample size to produce reliable results. | |||
* The results can be sensitive to the method of extraction and rotation used. | |||
* It assumes linear relationships between variables and factors. | |||
== Related pages == | |||
* [[Principal component analysis]] | * [[Principal component analysis]] | ||
* [[ | * [[Latent variable]] | ||
* [[Multivariate statistics]] | * [[Multivariate statistics]] | ||
[[Category:Statistical methods]] | |||
[[Category: | |||
Latest revision as of 10:52, 15 February 2025
Statistical method used to describe variability among observed variables
Overview[edit]
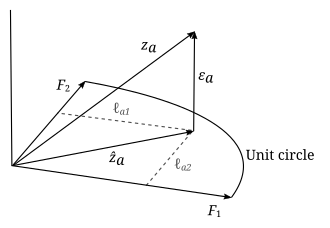
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. The observed variables are modeled as linear combinations of the potential factors, plus "error" terms. The information gained about the interdependencies can be used later to reduce the set of variables in a dataset.
History[edit]
Factor analysis originated in psychometrics and is used in behavioral sciences, social sciences, marketing, product management, operations research, and other applied sciences that deal with large quantities of data. The method was first introduced by Charles Spearman in the early 20th century.
Types of Factor Analysis[edit]
There are two main types of factor analysis:
- Exploratory Factor Analysis (EFA): Used to identify the underlying relationship between measured variables. It is often used when the researcher does not have a preconceived idea of the structure or number of factors.
- Confirmatory Factor Analysis (CFA): Used to test the hypothesis that the relationships between observed variables and their underlying latent constructs exist. It is often used when the researcher has a specific idea about the structure or number of factors.
Applications[edit]
Factor analysis is widely used in various fields:
- In psychology, it is used to identify latent constructs such as intelligence, personality traits, and other psychological phenomena.
- In marketing, it helps in identifying underlying factors that affect consumer behavior and preferences.
- In finance, it is used to identify factors that affect stock prices and market trends.
Methodology[edit]
The process of factor analysis involves several steps:
1. Data Collection: Gather data on the variables of interest. 2. Correlation Matrix: Compute the correlation matrix of the variables. 3. Extraction of Factors: Use methods such as principal component analysis or maximum likelihood to extract factors. 4. Rotation: Apply rotation methods like varimax or promax to achieve a simpler and more interpretable factor structure. 5. Interpretation: Analyze the factor loadings to interpret the factors.
Limitations[edit]
Factor analysis has several limitations:
- It requires a large sample size to produce reliable results.
- The results can be sensitive to the method of extraction and rotation used.
- It assumes linear relationships between variables and factors.