Convex hull

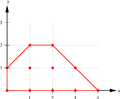
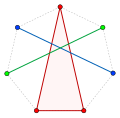
Convex Hull is a fundamental concept in the field of computational geometry and has applications in various fields such as computer graphics, pattern recognition, and robotics. It refers to the smallest convex set that contains a given set of points in a Euclidean space. In simpler terms, if one imagines each point as a peg on a board, the convex hull can be visualized as the shape formed by a rubber band stretched around the outermost pegs.

Definition

A set of points in a Euclidean space is said to be convex if, for every pair of points within the set, the line segment connecting them lies entirely within the set. The convex hull of a set of points is the smallest convex set that encompasses all the points. Mathematically, for a given set of points X, the convex hull is the set of all convex combinations of points in X.

Algorithms

Several algorithms exist for computing the convex hull of a set of points, each with its own computational complexity and suitability for different scenarios.

• Graham's Scan: An efficient algorithm for computing the convex hull of a set of points in the plane. It has a time complexity of O(n log n), where n is the number of points.
• Jarvis's March: Also known as the gift wrapping algorithm, it is simpler but less efficient than Graham's Scan, with a worst-case time complexity of O(nh), where h is the number of points on the hull.
• QuickHull: A method inspired by the quicksort algorithm, with an average time complexity of O(n log n), but it can degrade to O(n²) in the worst case.
• Chan's Algorithm: Combines the ideas of Graham's Scan and Jarvis's March to achieve an optimal O(n log h) time complexity.

Applications

The concept of a convex hull is widely applied in various domains:

• Computer Graphics: Used in algorithms for pattern recognition, image processing, and collision detection.
• Robotics: In motion planning and obstacle avoidance, the convex hull can represent the shape of objects or the environment.
• Geographical Information Systems (GIS): For defining the boundaries of geographical entities like lakes, forests, or urban areas.
• Data Analysis: Convex hulls can help in understanding the shape and distribution of datasets.

See Also

• Computational Geometry
• Euclidean Space
• Convex Set
• Graham's Scan
• Jarvis's March
• QuickHull
• Chan's Algorithm

References

This computer science-related article is a stub. You can help WikiMD by expanding it.

• 

  Extreme points of a set

• 

  Convex hull illustration

• 

  3D Convex Hull

• 

  Convex_hull

• 

  Convex hull example

• 

  Convex hull of a simple polygon

• 

  Convex_hull

• 

  Convex_hull

• 

  Convex_hull

• 

  Convex hull of Mg–C system